Question

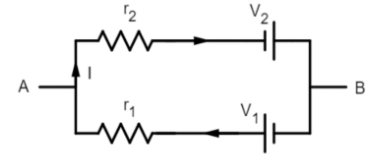
The emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emfs $V_1$ and $V_2$ and internal resistances $r_1$ and $r_2$ respectively, with polarities as shown in the figure are given by $\dfrac{V_1 r_2 – V_2 r_1}{r_1 + r_2}$ and $\dfrac{r_1 r_2}{r_1 + r_2}$:
A.True
B.False

Answer 1

Hint: The only tools required to verify this problem is Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL). In other words, apply KCL to one of the terminals A or B and determine the equivalent current flowing through the circuit. Then, short the batteries and find out the equivalent resistance of the circuit. Remember that though the resistances seem to be in series in the loop, the whole point of shorting the batteries is to see how they’d behave in the equivalent circuit. Now that you have both equivalent resistance and equivalent current, use Ohm’s Law to find the equivalent voltage and verify your answer.
Formula Used:
Kirchhoff’s Current Law (KCL): $I_{entering} + I_{exiting} = 0$, where $I_{entering}$ is the sum of all currents entering a junction in a circuit and $I_{leaving}$ is the sum of all currents leaving the same junction.
Kirchhoff’s Voltage Law (KVL): $\Sigma V =0$, which denotes that the algebraic sum of all voltages in any closed loop must be equal to zero.

Complete answer:
Let us begin by first assuming that terminals A and B are connected:

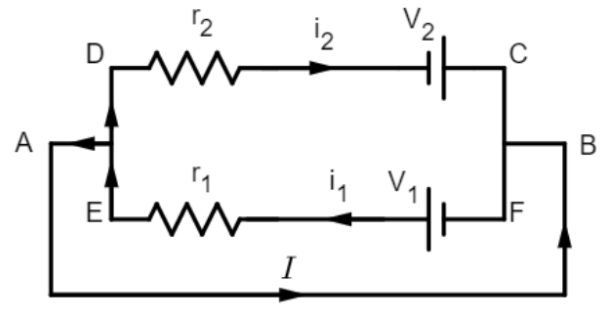
Now, when they are connected, let us assume that some current $I$ flows from A to B.
At the node of terminal A, we can apply Kirchhoff’s Current Law (KCL) which suggests that the algebraic sum of all currents entering and leaving a node must be equal to zero. From the diagram, we see that at node A, applying KCL gives us:
$\Rightarrow i_1 = I + i_2 \Rightarrow I = i_1 – i_2$
Now, let us bring in Kirchhoff’s Voltage Law (KVL) which suggests that the sum of all voltages around any closed loop in a circuit must be equal to zero. Since our circuit consists of a closed loop(s), let us apply KVL and see how it goes from there.
Applying KVL in the loop CDABC of our circuit we get:
$V_2 – i_2 r_2 = 0 \Rightarrow i_2 = \dfrac{V_2}{r_2}$
Applying KVL in the loop FEABF of our circuit we get:
$V_1 – i_1 r_1 = 0 \Rightarrow i_1 = \dfrac{V_1}{r_1}$
Applying what we got from KCL and KVL together we get:
$\Rightarrow I = i_1 - i_2 = \dfrac{V_1}{r_1}-\dfrac{V_2}{r_2}$
This is our equivalent current.
Now we short circuit our two batteries to see how our resistors behave. We deduce that the resistors are in fact parallel to each other when connected between terminals A and B and thus their equivalent resistance will be:
$\dfrac{1}R_{eq} = \dfrac{1}{r_1} +\dfrac{1}{r_2} = \dfrac{r_1 +r_2}{r_1 r_2}$
$\Rightarrow R_{eq} = \dfrac{r_1 r_2}{r_1 + r_2}$
Now that we have our equivalent resistance and equivalent current, we can find the equivalent voltage by:
$V_{eq} = IR_{eq} = \left(\dfrac{V_1}{r_1}-\dfrac{V_2}{r_2}\right) \times \left(\dfrac{r_1 r_2}{r_1 + r_2}\right) = \left(\dfrac{V_1 r_2 - V_2 r_1}{r_1 r_2}\right) \times \left(\dfrac{r_1 r_2}{r_1 + r_2}\right)$
$\Rightarrow V_{eq} = \dfrac{V_1 r_2 – V_2 r_1}{r_1 + r_2}$
Both $V_{eq}$ and $R_{eq}$ agree with the expressions given in the question.

Therefore, the correct choice would A.True.

Note:
Though we looked at KCL and KVL from a quantitative perspective, it is important to understand what they mean in a physical sense.
KCL signifies conservation of charge since the law basically suggests that the sum of currents entering a node must be equal to the sum of currents leaving the node, which means that electric charges are neither ambiguously lost nor mysteriously added but remains the same in an isolated system.
KVL signifies conservation of energy since the total energy in a system remains constant, though it may be transferred between components of the system in the form of electric potential and current.