Question

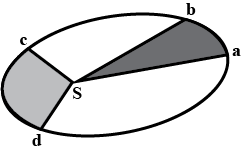
The elliptical path of a planet about the sun is shown in the given figure. The two shaded parts have equal area. If \[{t_1}\,and\,{t_2}\] be the time taken by the planet to go from a to b and from c to d respectively.

(A) ${t_1}\, > \,{t_2}$
(B) ${t_1}\, = \,{t_2}$
(C) ${t_2}\, > \,{t_1}$
(D) Insufficient information to deduce the relation between ${t_1}\,and\,{t_2}$

Answer 1

Hint: First of all we should know about the Kepler’s laws. Kepler's laws describe the orbits of planets around the sun or stars around a galaxy in classical mechanics. These laws are mainly used to predict the orbits of the objects such as asteroids and the comets, and in the discovery of dark matter in the Milky Way these laws were pivotal.

Complete step by step solution:
Second law of Kepler states that a planet moves in its ellipse such that making the line between it and the Sun placed at a focus sweeps out equal areas in equal times. It means that the radius vector sweeps equal areas in an equal interval of time from the sun to a planet.
Hence from the Kepler’s Second Law, we can say that the option B is correct. Hence ${t_1}\, = \,{t_2}$
From this law, it may be observed further that the angular momentum of any planet about an axis through the Sun and perpendicular to the orbital plane is also unchanging.

Note:
Kepler's Second Law is valuable because it gives a quantitative statement about how fast or slow the object will be moving at any point in its orbit. When the planet is closest to the Sun, at perihelion, then by the second Law of Kepler it will move the fastest and when the planet is most distant from the Sun, at aphelion, it will move the slowest.