Question

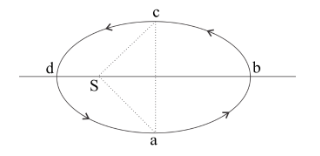
The elliptical path ABCD of a planet around the sun S is shown in the given figure. So the area of the triangle CSA is $\dfrac{1}{4}$ the area of the ellipse, with DB as major axis and CA as minor axis. If ${t_1}$ is the time taken for planet to go over the path ABC and ${t_2}$ for path taken over CDA then:

A) ${t_1} = 4{t_2}$
B) ${t_1} = 2{t_2}$
C) ${t_1} = {t_2}$
D) ${t_1} = 3{t_2}$

Answer 1

Hint:Kepler’s second law states that a planet sweeps out equal areas in equal times, that is, the area divided by time, called the areal velocity, is constant.

Complete step by step answer:
-Since area of triangle CSA is $\dfrac{1}{4}$of total area of ellipse, therefore:  
Area of CDAS = $\dfrac{1}{3}$​Area of ABCS.
-Now that from Kepler's second law areal velocities of the planets are constant which essentially means planets cover equal area in equal time intervals.
-Hence, Time taken in covering path ABC and path CDA will be in proportion to their respective enclosed areas.
-Hence ${t_1} = 3{t_2}$. Therefore the (d) statement is correct.

Note: Kepler’s three laws of planetary motion can be stated as follows:
(1) All planets move about the Sun in elliptical orbits, having the Sun as one of the foci.
(2) A radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time.
(3) The squares of the sidereal periods (of revolution) of the planets are directly proportional to the cubes of their mean distances from the Sun. From Kepler’s second law, it may be observed further that the angular momentum of any planet about an axis through the Sun and perpendicular to the orbital plane is also unchanging.