Question

The electric field $E$ is uniform in the shaded area and makes an angle $\theta $ with the normal. The conductivity of the material in which the area $S$ lies is $\sigma $. The electric current flowing out of the shaded area is

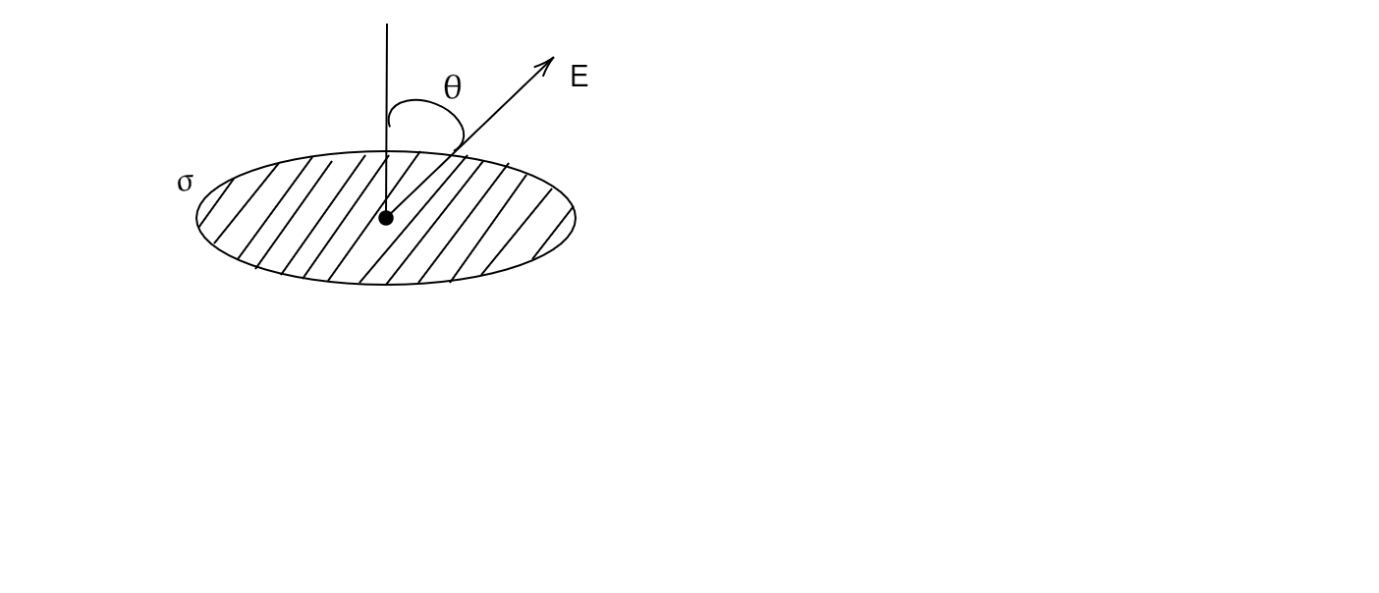
A.$\sigma ES\cos \theta $
B.$\sigma ES{\cos ^2}\theta $
C.$\sigma ES\sin \theta $
D.$\sigma ES{\sin ^2}\theta $

Answer 1

Hint: This is the question from the topic of electromagnetics. We have been given an enclosed area that has electric field E and conductivity $\sigma $ . so we will use ohm’s law which gives the relation between current density, electric field, and conductivity. With the help of current density, we will find the required current flowing out of the shaded area by using the relation between them.

Complete answer:
By using ohm’s law
\[I = \dfrac{V}{R}\] Where $I$ is the current $V$ is the voltage and $R$ is the resistance in a conductor.
$ \Rightarrow J = \dfrac{I}{A} = \dfrac{V}{{RA}}$We know,
Where $J$ is the current density in a resistive material at a particular point
As, $R = \dfrac{{\rho l}}{A}$ where $\rho $ is the resistivity $l$ is the length and $A$ is the area of cross-section of material.
As, $V = El$ where $E$ is the electric field.
Putting all this in the above equation we get
$J = \dfrac{E}{\rho } = \sigma E$
Where $\sigma $ (sigma) is a material-dependent characteristic termed conductivity.
Using the relation between current and current density. We know that Current is equal to the dot product of the current density and the area vector.
$I = J.ds$
$ \Rightarrow I = JS\cos \theta $
Therefore, $J = \dfrac{I}{{S\cos \theta }}$
$ \Rightarrow \dfrac{I}{{S\cos \theta }} = \sigma E$
$ \Rightarrow I = \sigma ES\cos \theta $
So The electric current flowing out of the shaded area is $I = \sigma ES\cos \theta $

Hence, option A) $\sigma ES\cos \theta $ is the correct option.

Note:
Area vector is always normal to the surface of the object. When they say they're giving an angle, they're saying they're giving an angle between the area vector and the electric field.
The capacity of a material to enable charge carriers to travel through it is measured by conductivity; the ability of a substance to prohibit charge carriers from moving through it is measured by resistance $\therefore \sigma = \dfrac{1}{\rho }$