Question

The effective resistance between the points A and B in the circuit shown in Figure will be:

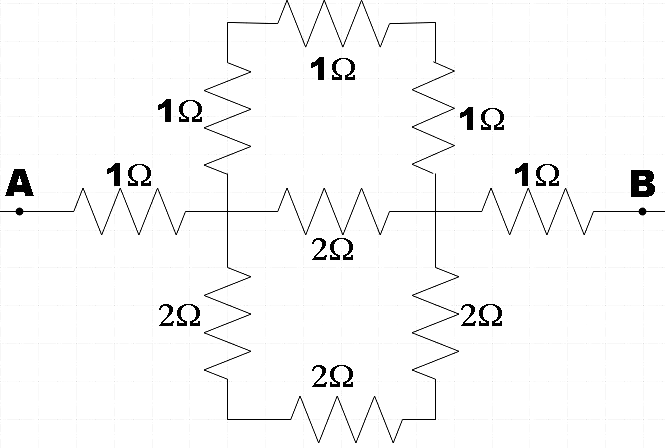
A.$6\Omega $
B.$3\Omega $
C.$15\Omega $
D.$10\Omega $

Answer 1

Hint: You could find the effective resistance of the whole combination by dealing it part by part. Firstly, you could go for the loop part. You could find it for the series connection in the upper half and lower half of the loop resulting in a parallel combination of three resistors. At the end you will be left with three resistors and the sum of their resistances will be the effective resistance of the given combination.
Formula used:
For series combination,
${{R}_{eff}}={{R}_{1}}+{{R}_{2}}$
For parallel combination,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$

Complete answer:
In the question, we are given a combination of resistors and are asked to find the effective resistance across the points A and B.
Just like any other problem dealing with a combination of resistors, we could deal with it part by part and thus reduce the complex combination to a rather simple one.
Firstly, let us consider the closed loop part. In the upper half of that part we have three $1\Omega $ resistors connected in series. For a series combination, we know that the effective resistance is given by the sum of the individual resistances, so,
${{R}_{eff}}=1\Omega +1\Omega +1\Omega $
$\therefore {{R}_{eff}}=3\Omega $ ………………………………………… (1)
Similarly, in the lower half of the loop, we have, three$2\Omega $ resistors and their effective resistance could be given by,
${{R}_{eff}}'=2\Omega +2\Omega +2\Omega $
$\therefore {{R}_{eff}}'=6\Omega $ …………………………………………… (2)
Now, we could redraw the given circuit as,

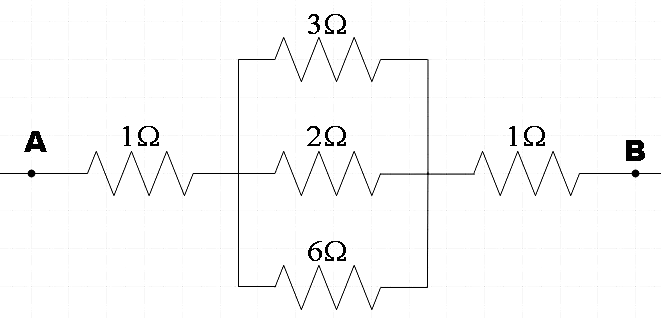
In the loop we have three resistors of resistances $3\Omega ,2\Omega $ and $6\Omega $ connected in parallel. We know that, for parallel connection, the effective resistance if given by,
$\dfrac{1}{{{R}_{eff}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}$
$\Rightarrow \dfrac{1}{{{R}_{eff}}}=\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{1}{6}$
$\Rightarrow \dfrac{1}{{{R}_{eff}}}=\dfrac{2+3+1}{6}=\dfrac{6}{6}$
$\therefore {{R}_{eff}}=1\Omega $
Now that we have found the effective resistance of the whole loop to be $1\Omega $, we are left with three $1\Omega $ resistors across points A and B.
So the effective resistance across A and B could be given by the sum of these three resistances. That is,
${{R}_{AB}}=1\Omega +1\Omega +1\Omega $
$\therefore {{R}_{AB}}=3\Omega $
Therefore, we found the effective resistance across A and B to be $3\Omega $.

Hence, option B is found to be the correct answer.

Note:
In the questions where we are asked to find the effective resistance, you could firstly simplify the complex combination into series and parallel connections. Sometimes, you may find other simplifications where we have a Wheatstone bridge in the combination. We could then find the effective resistance for simple series and parallel connections and hence the effective resistance of the combination.