Question

The eccentricity of an ellipse, with its Centre at the origin, is $\dfrac{1}{2}$. If one of the directrices is $x=4$ , then the equation of the ellipse is:

Answer 1

Hint: From the question given we have been asked to find the equation of the ellipse having Centre at the origin, with eccentricity $\dfrac{1}{2}$, and one of the directrices is $x=4$. as we know that the general equation of ellipse having centre as origin is$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$, here $a>ba>b$ because the directrix is parallel to y axis. And also, we know that the formula ${{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)$, and also, we know that the directrix x-coordinate will be equal to $\dfrac{a}{e}$. From all this we will get the equation of ellipse.

Complete step by step solution:
From the question given that the eccentricity of the ellipse having centre as origin is,
$\Rightarrow e=\dfrac{1}{2}$
And also given that the one of the directrices is
$\Rightarrow x=4$
As we know that the x-coordinate of directrix is equal to
$\Rightarrow \dfrac{a}{e}$
By this we will get the value of “a” as we know the value of e,
$\Rightarrow \dfrac{a}{e}=4$
$\Rightarrow a=4e$
$\Rightarrow a=4\times \dfrac{1}{2}$
$\Rightarrow a=2$
To find the value of “b” as we know that the formula,
$\Rightarrow {{b}^{2}}={{a}^{2}}\left( 1-{{e}^{2}} \right)$
Now, by substituting the values in their respective position we will get,
$\Rightarrow {{b}^{2}}={{\left( 2 \right)}^{2}}\left( 1-{{\left( \dfrac{1}{2} \right)}^{2}} \right)$
By simplifying further, we will get,
$\Rightarrow {{b}^{2}}=4\left( 1-\dfrac{1}{4} \right)$
$\Rightarrow {{b}^{2}}=4\left( \dfrac{3}{4} \right)$
$\Rightarrow {{b}^{2}}=3$
Therefore, we know that the general equation of the ellipse having centre as origin is,
$\Rightarrow \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Now by substituting the values of “a” and “b”, we will get the required ellipse equation,
$\Rightarrow \dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{3}=1$
By further simplifying we will get,
$\Rightarrow 3{{x}^{2}}+4{{y}^{2}}=12$
Therefore, this is the required ellipse equation.
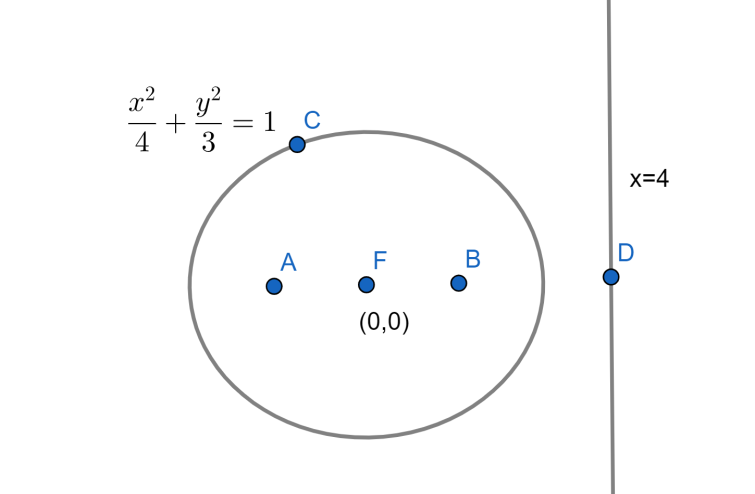
The figure would be as follows.

Note: students should recall the all the formulas of ellipse before doing this problem, students should know also note that the general equation of ellipse having origin as $\left( h,k \right)$ is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$.