Question

The ear-ring of a lady shown in figure $ \left( {12 - E18} \right) $ has a $ 3cm $ long light suspension wire. (a) Find the time period of small oscillations if the lady is standing on the ground. (b) The lady now sits in a merry-go-round moving at $ 4m{s^{ - 1}} $ in a circle of radius $ 2m $ . Find the time period of small oscillations of the ear-ring.

Answer 1

Hint :In order to solve this question, we are going to first find the time period of the earrings for the lady standing on the ground from the formula based on length and acceleration. And in the second part also, we first find the total acceleration from gravity and the centripetal acceleration and then, the time period.
The time period of the oscillations is calculated as
 $ T = 2\pi \sqrt {\dfrac{l}{a}} $
Where, $ a $ is acceleration
Centripetal force
 $ F = \dfrac{{m{v^2}}}{r} $

Complete Step By Step Answer:
It is given that the length of the light suspension wire is
 $ l = 3cm $
Converting the length into meter, we get
 $ l = 0.03m $
The time period of the oscillations is calculated as
 $ T = 2\pi \sqrt {\dfrac{l}{g}} $
Putting the values, we get
 $ T = 2\pi \sqrt {\dfrac{{0.03}}{{9.8}}} = 0.34\sec $
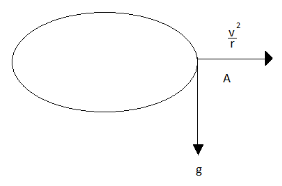
(b) Now, when this lady sits on a merry-go-round, one more force that acts on the earring now is the centripetal force
 $ F = \dfrac{{m{v^2}}}{r} $
Thus, the acceleration is calculated as
 $ a = \dfrac{{{v^2}}}{r} $
Putting the values, we get
 $ a = \dfrac{{{4^2}}}{2} = 8m{s^{ - 2}} $
Net acceleration due to the gravity and the centripetal acceleration is:
 $ A = \sqrt {{g^2} + {a^2}} $
Putting values, we get
 $ A = \sqrt {100 + 64} = 12.8m{s^{ - 2}} $
Now, the time period is given by
 $ T = 2\pi \sqrt {\dfrac{l}{A}} $
Putting values, we get
 $ T = 2\pi \sqrt {\dfrac{{0.03}}{{12.8}}} = 0.30\sec $

Note :
A centripetal force is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous center of curvature of the path. The net acceleration consists of two components, gravity and centripetal acceleration.