Question

The driver of a car moving towards a rocket launching pad with a speed of $6m{s^{ - 1}}$ observed that the rocket is moving with a speed of $10m{s^{ - 1}}$ the upward speed of the rocket as seen by the stationary observer is
A. $4m{s^{ - 1}}$
B. $6m{s^{ - 1}}$
C. $8m{s^{ - 1}}$
D. $11m{s^{ - 1}}$

Answer 1

Hint: The resultant vector or the velocity of the rocket observed by the driver is the square root of the sum of the square of velocity of the car and square of velocity of the rocket observed by the stationary observer.

Complete step by step solution:
 The driver of a car is moving towards a rocket launching pad with a speed of $Vc = 6m{s^{ - 1}}$ . The driver observed that the rocket is moving with a speed of ${V_{rc}} = 10m{s^{ - 1}}$. Let the upward speed of the rocket as seen by the stationary observer i.e, the observer who is in a rest position be Vo.

According to parallelogram law of vectors, when two vectors acting simultaneously at a point can be represented both in magnitude and direction by the two adjacent sides of a parallelogram drawn from the same point, then the resultant vector is represented both in magnitude and direction by the diagonal of the parallelogram passing through that point.

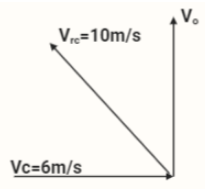
In the above figure, Vo represent the direction of rocket as observed by a stationary observer, Vc represent the direction at which the car is moving towards the rocket and ${V_{rc}}$ represent the relative velocity of the rocket as observed by the driver of a car.
The magnitude of resultant vector is given by the formula,
${V_{rc}} = \sqrt{ {{V_c}^2} + {{V_o}^2} + 2\left( {V_c} \right)\left( {Vo} \right)\cos \theta } $ where $\theta $ is the angle formed between Vc and Vo.
${V_{rc}} = \sqrt {{{\left( { - {V_c}} \right)}^2} + {{V_o}^2} + 2\left( { - {V_c}} \right) {V_o}\cos {{90}^ \circ }} $ as the direction of Vc is opposite to the direction of side of parallelogram and the angle between the two adjacent side is ${90^ \circ }$ .
${10^2} = {\left( { - 6} \right)^2} + {{V_o}^2} + 0$ as $\cos {90^ \circ } = 0$ .
$\Rightarrow 100 = 36 + { {V_o}^2}$
$\Rightarrow 100 - 36 = {{V_o}^2}$
$\Rightarrow \sqrt {64} = {V_o} $
$\therefore {V_o} = 8m{s^{ - 1}}$
Hence, the upward speed of the rocket as seen by the stationary observer is $8m{s^{ - 1}}$

Therefore, option C is correct.

Note: Kindly don’t get confused about the sign of ${V_c}$ as it is taken negative instead of positive because the direction of this vector is opposite to the direction at which side of the parallelogram is aligned in a vector. In a parallelogram law of vectors, the two vectors start or arise from the same point. Remember the formula of the resultant vector as it will be helpful to find the velocity in this case easily.