Question

The domain of $f(x)=\cot 5x$ is .
(a)$R-\dfrac{n\pi }{2}$
(b)$R-\dfrac{n\pi }{5}$
(c)$R-n\pi $
(d)$R+n\pi $

Answer 1

Hint: To start with the question, convert cot5x in terms of sin5x and cos5x. Then use the property that trigonometric ratios are periodic functions and the fact that a number is defined if and only if the denominator is not equal to zero.

Complete step-by-step answer:

Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.

First, let us start with the graph of sinx.

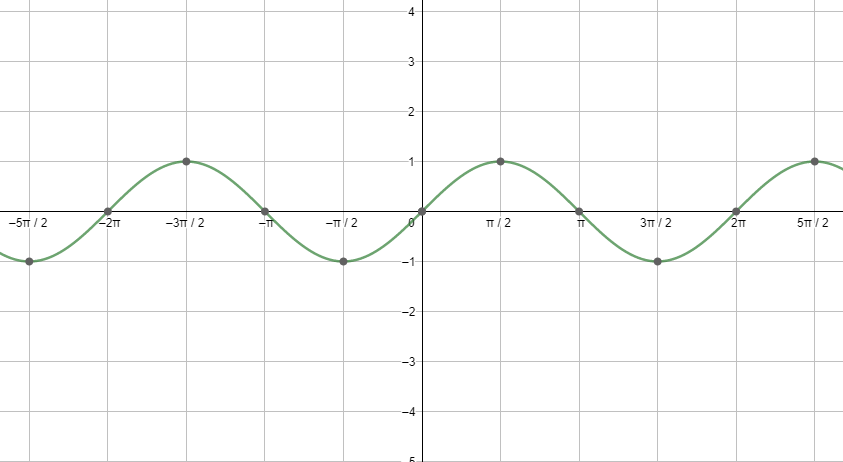
Next, let us see the graph of cosx.

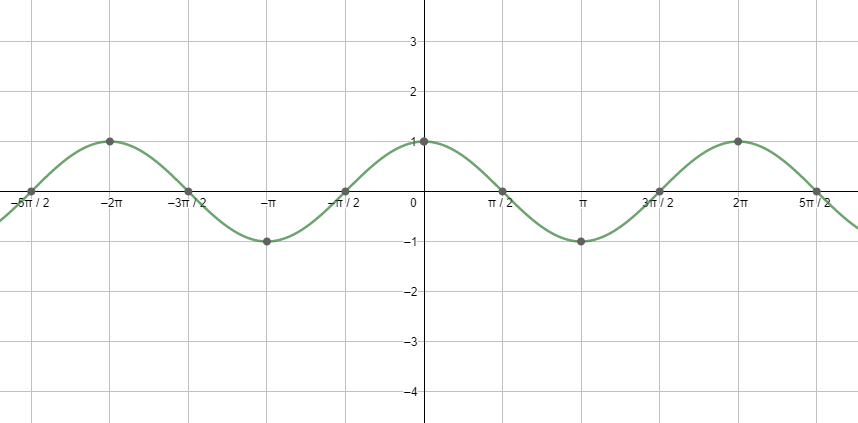
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ $ .

Now to start with the question we let 5x to be t. On doing so cot5x becomes $\cot t$ .

We know that $\cot t=\dfrac{\cos t}{\sin t}$ . We also know that for $\cot t$ to be defined, the denominator must not be equal to zero i.e., sint must not be equal to zero.

But from the graph of sinx we have that sinx is zero for all the multiples of $\pi $ . Therefore we can say that it can be anything except a multiple of $\pi $ .

Now from the above result we can say that:

$t\ne n\pi $

$\therefore 5x\ne n\pi $

\[\Rightarrow x\ne \dfrac{n\pi }{5}\]

So, from this result, we can conclude that for cot5x to be defined, x can be any real number except a multiple of $\dfrac{\pi }{5}$ . Hence, the answer to the above question is option (b) $R-\dfrac{n\pi }{5}$ .


Note: It is useful to remember the graph of the trigonometric ratios along with the signs of their values in different quadrants. For example: sine is always positive in the first and the second quadrant while negative in the other two.