Question

The distance between a node and an anti-node is
A. \[2\lambda \]
B. \[\lambda \]
C. \[\dfrac{\lambda }{2}\]
D. \[\dfrac{\lambda }{4}\]

Answer 1

Hint: From definition we know that an antinode and a node is \[\dfrac{1}{2}\]the distance between \[2\]consecutive nodes. Then we solve it using the formula \[\lambda = 2(2 \times \]Distance between a node and an antinode\[)\].

Complete step by step solution:
Here,
From the definition we know that,
The wavelength of a wave is defined as having twice the distance between two consecutive nodes and antinodes.
Now,
The distance between an antinode and a node is \[\dfrac{1}{2}\] the distance between \[2\] consecutive nodes.
Therefore,
\[\lambda = 2(2 \times \] Distance between a node and an antinode\[)\]
Hence,
The required distance is \[\dfrac{\lambda }{4}\]

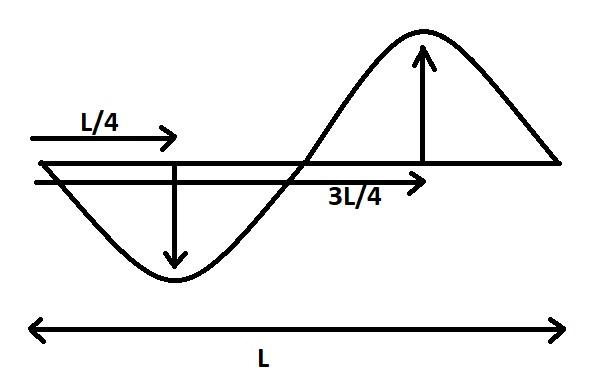
Note: From definition we know that an antinode is the place where the wave’s maximum amplitude is generated by positive interference of the incoming and reflected waves. A node, by comparison, is the position where destructive interference reduces the amplitude of the wave to zero.