Question

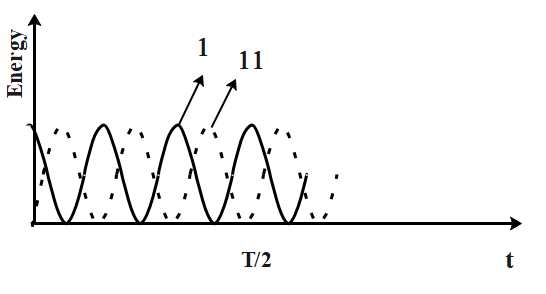
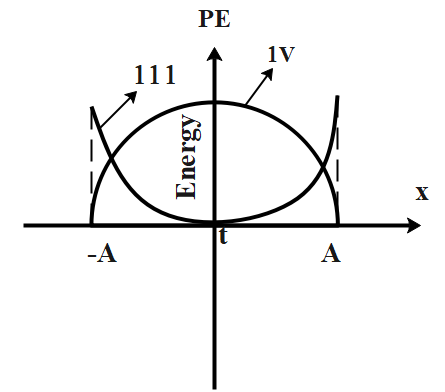
The displacement of linear harmonic oscillator is given by \[x=A\cos \omega t\]. The curves showing the variation of the potential energy with t and x (see figure) are displayed respectively by:
(a) 1 and 3
(b) 1 and 4
(c) 2 and 3
(d) 2 and 4

Answer 1

Hint: The above question can be solved by finding out the relationship of potential energy with displacement and time period. Since there is a direct formula to find potential energy if angular frequency is given and we will use the equation connecting angular frequency and time period.

Complete answer:
For a linear harmonic oscillator, the angular frequency is given by the formula:
$\omega =\dfrac{2\pi }{T}$
Where,
$\omega =$Angular Frequency (Angular displacement per unit time)
$T=$Time period (time taken to complete one oscillation)
The Potential Energy is given by the formula:
\[U=\dfrac{1}{2}m{{\omega }^{2}}{{x}^{2}}\]
From the formula showing the relation between angular frequency and time period, we know that
$\omega =\dfrac{2\pi }{T}$
Squaring the terms,
\[{{\omega }^{2}}=\dfrac{4{{\pi }^{2}}}{{{T}^{2}}}\]
Substituting this in the potential energy equation, we get,
\[U=\dfrac{1}{2}m{{\omega }^{2}}{{x}^{2}}\]
\[U=2{{\pi }^{2}}\dfrac{m{{x}^{2}}}{{{T}^{2}}}\]
Hence, we found out that potential Energy is directly proportional to Square of distance and inversely proportional to square of time period.
Now, from the first curve, (1) shows that when time =0, i.e before releasing the particle is at maximum potential energy. This shows the inverse relationship between Time period and Potential energy.
From the second curve, (3) shows that Energy is maximum at extreme positions A and -A and minimum at mean position. This shows that energy and displacement is directly proportional.

Hence, the answer is option (a) 1 and 3 is the final answer.

Note:
A particle is said to execute simple harmonic motion if it moves to and from about a mean position under the action of a restoring force which is directly proportional to its displacement from the mean position and is directed towards mean position.