Question

The direction $\left( \theta \right)$ of $\overrightarrow{E}$ at point P due to uniformly charged finite rod will be

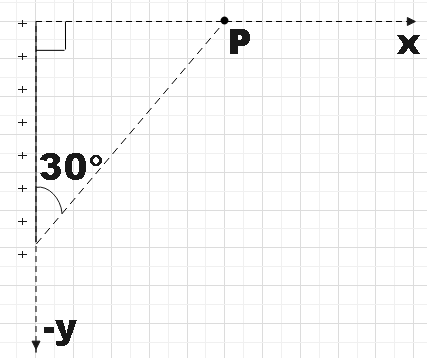
A. at angle $30{}^\circ $ from x-axis
B. $45{}^\circ $ from x-axis
C. $60{}^\circ $ from x-axis
D. none of these

Answer 1

Hint: As a first step find the angle subtended by the finite rod at the point P by using the property of angle sum of triangles. Then, you could assume the net charge to be concentrated at the centre most point of the rod. Then, knowing how the electric field would be directed for a positively charged rod and simple geometry you could solve the question.

Complete answer:
In the question, we are given a finite rod which is positively charged. We are given one of the angles in the triangle to be$30{}^\circ $. Now, from angle sum property of triangles we have,
$90+30+x=180$
Where, x is the angle subtended by the finite rod at the point marked P.
$x=60{}^\circ $
Now, we could recall that the electric field direction is given from positive to negative and so the electric field will be directed outward at point P.
Now, let us assume that the charge is concentrated at the midpoint of the given finite rod. So, we know from basic geometry that the line bisecting the finite rod will bisect the angle subtended at the point P.

In the above figure we see that the electric field line the angle x which is the angle subtended by the finite rod at point P. So, we could write that,
$x=2\theta =60{}^\circ $
$\therefore \theta =30{}^\circ $
Hence, we found that the direction $\left( \theta \right)$ of $\overrightarrow{E}$ at point P due to uniformly charged finite rod will be at angle $30{}^\circ $ from x-axis.

Option A is correct.

Note:
We have solved the above question by simply having a strong grasp on basic geometry and also based on some quite obvious assumptions. Very similar to assuming the centre of mass at the geometric centre of certain objects we have here assumed the net charge to be concentrated at the centre of the finite rod given.