Question

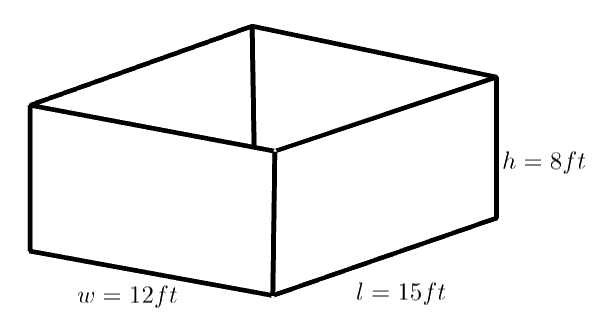
The dimensions of a room are $l=15ft,w=12ft$ and $h=8ft$ . How many square feet of wallpaper will be required to cover the walls of this room?

Answer 1

Hint: In this problem, we have to first find the dimensions of the floor which will be $15\times 12ft$ . Now, since all the walls share a common side with the floor, the walls will be of length $15ft$ or $12ft$ and height $8ft$ . We now find the individual area of the walls by the area of a rectangle formula and then add all the areas.

Complete step-by-step solution:
The given dimensions of the room are $l=15ft,w=12ft$ and $h=8ft$ . This means that the floor of the room will have its length as $l=15ft$ and its width as $w=12ft$ . The floor is a rectangle with the aforesaid length and width. The four walls will be situated on the floor at its edges. This means that every wall will share a common side with the floor.
The floor being a rectangle, there will be two pairs of sides, one being the length of $l=15ft$ and the other being the width of length $w=12ft$ . And, since the walls share one common side with the floor, there will also be two pairs of walls, one having a length of $15ft$ and the other having a length of $12ft$ . The heights of all the four walls are the same, which is $h=8ft$ . Thus, we have four walls which are four rectangles.
We know that the area of a rectangle is $length\times width$ . So, the area of the wall with length $15ft$ and height $h=8ft$ will be $15\times 8=120~sq.\text{ }ft$ and the area of the wall with length $12ft$ and height $h=8ft$ will be $12\times 8=96~sq.\text{ }ft$ . The total area of the four walls will be $2\times \left( 120+96 \right)=432sq.ft$ .
Therefore, we can conclude that $432$ square feet of wallpaper will be required to cover the walls.

Note: In these types of problems, we should carefully note that the area of which parts are required. The question may sometimes demand the combined area of the ceiling and the walls, which we may overlook and get our answers wrong. Also, at last, we must remember to add all the individual areas to get the combined area.