Question

The dimensions of a field are 15m by 12m. A pit 7.5m long, 6m wide and 1.5m deep is dug at one corner of the field. The earth removed is evenly spread over the remaining area of the field. Calculate the rise in the level of the field.

Answer 1

Hint: We can find the volume of earth removed by calculating the volume of the pit. The remaining area after taking the pit can be found by subtracting the area of the pit from the total area of the field. Then we can find the height by dividing the volume with the remaining area of the field.

Complete step-by-step answer:

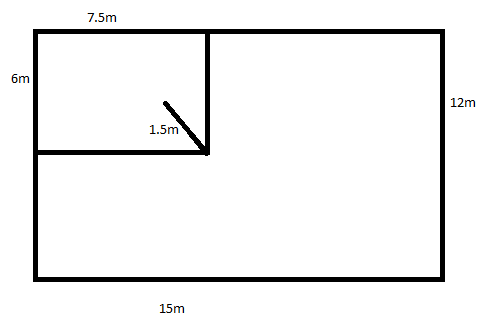
It is given that the pit is 7.5m long, 6m wide and 1.5m deep. So the volume of the earth removed will be equal to the volume of the pit. It is given by,
 $V = l \times b \times h$
On substituting the values, we get,
 $ \Rightarrow V = 7.5 \times 6 \times 1.5$
On taking the product, we get,
 $ \Rightarrow V = 67.5{m^3}$
This volume of earth is spread across the remaining area of the land.
The remaining area is given by the total area of the field minus the area of pit.
It is given that dimensions of the field are 15m by 12m.
So its area is given by,
 ${A_{field}} = l \times b$
On substituting the values, we get,
 $ \Rightarrow {A_{field}} = 15 \times 12$
On multiplication we get,
 $ \Rightarrow {A_{field}} = 180{m^2}$
It is given that the pit is 7.5m long and 6m wide. So, its area is given by,
 ${A_{pit}} = l \times b$
On substituting the values, we get,
 $ \Rightarrow {A_{pit}} = 7.5 \times 6$
On simplification we get,
 $ \Rightarrow {A_{pit}} = 45{m^2}$
Now the remaining area is given by,
 $A = {A_{field}} - {A_{pit}}$
On substituting the values we get,
 $ \Rightarrow A = 180 - 45$
On simplification we get,
 $ \Rightarrow A = 135{m^2}$
We know that volume is given by the product of height and area of the base.
Let h be the rise in level of the field.
 $ \Rightarrow V = A \times h$
On substitute the values, we get,
 \[ \Rightarrow 67.5 = 135 \times h\]
On rearranging, we get,
 \[ \Rightarrow h = \dfrac{{67.5}}{{135}}\]
On simplification we get,
 \[ \Rightarrow h = 0.5m\]
Therefore, the rise in level of the field is 0.5m.
Note: The concept of areas and volumes of rectangles and cuboids are used to solve this problem. We must know that the volume is the product of the base area and height. While finding the area of the pit, we must take the length and breadth properly. To find the base area we must subtract the area of the pit as it is given that only the remaining area is filled.