Question

The dimensions of a cuboid are 44cm, 21 cm, 12 cm. It is melted and a cone of height 24cm is made. Find the radius of its base.

Answer 1

Hint: - In this particular question find the volume of the cuboid and then equate that with the volume of the cone to find the radius of the base of the cone. Using formula \[\left( {{\text{Volume of cuboid}} = l \times b \times h} \right)\] and \[\left( {{\text{Volume of cone}} = \dfrac{1}{3}\pi {r^2}h} \right)\].

Complete step-by-step answer:
Now let us first assume that the radius of the base of the cone is equal to r cm.
   

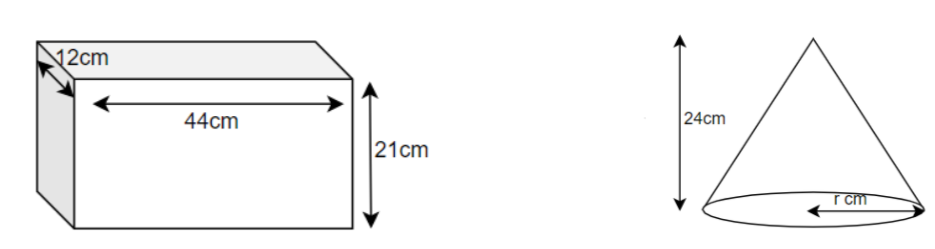
So, now we had to find the volume of the cone.
Now as we know that if the radius of the cone is r and height is h then its volume will be \[\dfrac{1}{3}\pi {r^2}h\].
So, the volume of the cone formed will be = \[\dfrac{1}{3}\pi {r^2}\left( {24} \right) = \left( {8\pi {r^2}} \right)c{m^3}\]
And the volume of the cuboid with dimensions l, b and h is calculated as \[l \times b \times h\].
So, the volume of the cuboid given will be \[44 \times 21 \times 12 = 11088c{m^3}\]
Now as we know that cuboid is melted and changed into a cone.
So, the volume of cuboid must be equal to the volume of the cone.
So, \[8\pi {r^2} = 11088\] ……………………………………. (1)
Dividing both sides of the above equation by \[8\pi \]. And then putting the value of \[\pi \] in it.
\[ \Rightarrow {r^2} = \dfrac{{11088}}{{8\left( {\dfrac{{22}}{7}} \right)}} = \dfrac{{77616}}{{176}} = 441\] ………………………………. (2)
Now taking the square root on both sides of the above equation.
\[ \Rightarrow r = \pm 21\]cm
Now the radius of the cone cannot be negative.
Hence, the radius of the cone formed will be $21 \text{cm}$.

Note: Whenever we face such types of questions the key concept is that the volume of both the solid remains same when one solid is melted and changed into another solid, So, first we had to assume the unknown dimension as variable. Like here radius = r. And after that we had to find the volume of the previous solid (here cuboid) and the solid after melting (cone). Using appropriate formulas and then equating them to get the required value of the variable. But remember that we had to neglect the negative value because the dimension can never be negative. This will be the easiest and most efficient way to find the solution to the problem.