Question

The dimensions of a car petrol tank are $50\text{ cm}\,\times \,32\,\text{cm }\times \,24\,\text{cm}$, which is full of petrol. If a car's average consumption is 15 km per litre, find the maximum distance that can be covered by the car.

Answer 1

Hint: We will apply the formula of the volume of the cuboid here so that we can solve the question further. This is because the petrol tank is in the form of a cuboid only. The formula of the cuboid is given by $\text{Volume of cuboid = length }\times \text{ breadth }\times \text{ height}$ which has the unit as a cubic unit. The unit is taken according to the question. Here, the unit is centimetres therefore, we will write the volume as cubic centimetres. Also, we will use the conversion here which is given by $1\,\text{litre}\,\text{=}\,\text{1000}\,\text{c}{{\text{m}}^{3}}$ to change the volume’s value to litres.

Complete step-by-step answer:
The required diagram for the petrol tank in the form of a cuboid is shown below.

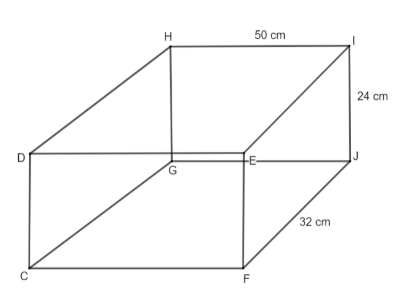
The dimensions of the car petrol tank are given by $50\text{ cm}\,\times \,32\,\text{cm }\times \,24\,\text{cm}$. Therefore, by the formula of the volume of the cuboid we will have the volume of the petrol. The formula is given as $\text{Volume of cuboid = length }\times \text{ breadth }\times \text{ height}$. Now, we will substitute the values of length as 50 cm breadth as 32 cm and the height as 24 cm. Thus, we will get,
$\begin{align}
  & \text{Volume of cuboid = }50\text{ cm }\times \text{ }32\text{ cm }\times \text{ }24\text{ cm} \\
 & \Rightarrow \text{Volume of cuboid = }50\text{ cm }\times \,768\,\text{c}{{\text{m}}^{2}} \\
 & \Rightarrow \text{Volume of cuboid = }38400\text{ c}{{\text{m}}^{3}} \\
\end{align}$
So, the volume of the petrol is 38400 cubic centimetres. Now, we will convert the unit of cubic centimetres into litres. This can be done by the formula, $1\,\text{litre}\,\text{=}\,\text{1000}\,\text{c}{{\text{m}}^{3}}$ or $1\,\text{c}{{\text{m}}^{3}}\,=\,\dfrac{1}{1000}\,\text{litres}$. Therefore, the volume of the cuboid is now carried out as
$\begin{align}
  & 38400\text{ c}{{\text{m}}^{3}}\,=\,38400\,\times \,1\,\text{c}{{\text{m}}^{\text{3}}} \\
 & \Rightarrow 38400\text{ c}{{\text{m}}^{3}}\,=\,38400\,\times \,\dfrac{1}{1000}\,\text{litres} \\
 & \Rightarrow 38400\text{ c}{{\text{m}}^{3}}\,=\,\dfrac{38400}{1000}\,\text{litres} \\
 & \Rightarrow 38400\text{ c}{{\text{m}}^{3}}\,=\,\dfrac{384}{10}\,\text{litres} \\
 & \Rightarrow 38400\text{ c}{{\text{m}}^{3}}\,=\,38.4\,\text{litres} \\
\end{align}$
Therefore, the volume of the petrol in litres is 38.4. As we are given that the car’s average consumption is 15 km per litre which actually, means that in 1 litre the car can cover the distance of 15 km. We will now use the unitary method here.
By the unitary method we have that in 1 litre the car can cover the distance of 15 km.
So, in 38.4 litres the car can cover a distance of 38.4 $\times $ 15 km. Or we can also write it as 576 km.
Hence, the maximum distance that a car can cover is 576 kilometres.

Note: Before solving the question we will notice the units that are given in the question. If the units are not the same then we will convert them into the same units and then we will solve further. Since, we are given the question that the car’s average consumption is 15 km per litre that is why we have changed the unit of cubic centimetres into litres in order to solve the question further. We also should know that difference between the words cube and cuboid. Some take the cube as a cuboid only which is wrong. By the dimensions that are given to us we can easily find out that the figure given to us is a cuboid.