Question

The difference in the value of ‘g’ at pole and at a latitude is \[\dfrac{3}{4}R{{\omega }^{2}}\] then latitude angle is:
(A). \[60{}^\circ \]
(B). \[30{}^\circ \]
(C). \[45{}^\circ \]
(D). \[95{}^\circ \]

Answer 1

Hint: Consider the earth as a sphere and find the forces are acting on the body placed on the surface. It will help to find the difference in weight happening due to the latitude variation. From this, we can find out the variation of acceleration due to gravity.

Formula Used:
Centrifugal force, \[mr{{\omega }^{2}}\], where m is the mass, r is the distance from the axis and \[\omega \] is the angular velocity.

Complete step-by-step answer:
The value of g will vary with the distance. As we know our Earth is an oblate shaped one. At the poles acceleration due to gravity will be maximum and at the equator, it will be minimal due to the variation of latitude angle. Here we have given the difference in the value of g at the pole and a latitude. That is \[\dfrac{3}{4}R{{\omega }^{2}}\].
Let us consider an object of mass m at a point P with latitude \[\theta \] as shown in the figure at the surface of the earth.

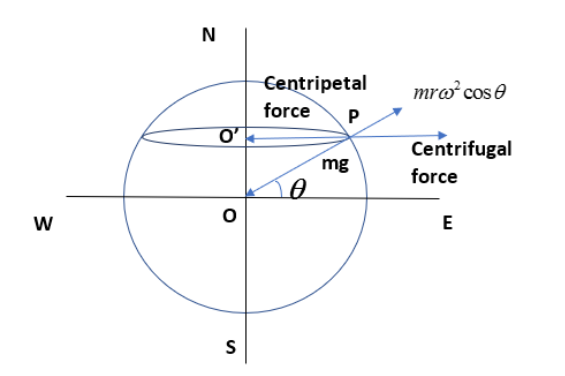
The distance of the point P from the O is the radius of the earth (R) while the distance of the point from \[{O}'\] is the distance of the point from the earth axis (r).
Due to rotational motion of the earth about its axis, the object will experience a centrifugal force of \[mr{{\omega }^{2}}\]. One of the rectangular components of the centrifugal force will be \[mr{{\omega }^{2}}\cos \theta \] and it will act along the radius of the earth.
The weight of the object acting along the inward direction and the \[mr{{\omega }^{2}}\cos \theta \] acting along the outward direction. Since these are two opposing forces, the difference between these two forces will give the actual weight of the body at that point.
\[m{{g}_{\theta }}=mg-mr{{\omega }^{2}}\cos \theta \]…………….(1), where m is the mass of the object, r is the distance between the axis of the earth and the point, g is the acceleration due to gravity and \[\theta \] is the latitude angle.
From the figure, you can say that,
\[\cos \theta =\dfrac{{O}'P}{OP}\]
\[\cos \theta =\dfrac{r}{R}\]
So we can write as,
\[r=R\cos \theta \]
We can substitute this value into equation (1).
\[m{{g}_{\theta }}=mg-mR\cos \theta {{\omega }^{2}}\cos \theta \]
We can reduce this expression as,
\[{{g}_{\theta }}=g-R{{\omega }^{2}}{{\cos }^{2}}\theta \]…………….(2)
At poles, the angle will be \[90{}^\circ \]. So the acceleration due to gravity will be maximum. So it will be equal to g. At the equator, the angle will be \[0{}^\circ \]. Hence the acceleration due to gravity will be minimum.
The difference in the values of g at the pole and specific latitude is given. It can be written as,
\[\Delta g=g-{{g}_{\theta }}\], where g is the acceleration due to gravity at poles and \[{{g}_{\theta }}\] is the acceleration due to gravity at a specific latitude of angle \[\theta \].
\[\Delta g=g-{{g}_{\theta }}=\dfrac{3}{4}R{{\omega }^{2}}\]
We can substitute equation (2) in this equation.
\[\Delta g=g-(g-R{{\omega }^{2}}{{\cos }^{2}}\theta )=\dfrac{3}{4}R{{\omega }^{2}}\]
\[R{{\omega }^{2}}{{\cos }^{2}}\theta =\dfrac{3}{4}R{{\omega }^{2}}\]
\[{{\cos }^{2}}\theta =\dfrac{3}{4}\]
\[\cos \theta =\sqrt{\dfrac{3}{4}}\]
\[\cos \theta =\dfrac{\sqrt{3}}{2}\], It will be possible only for \[\theta =30{}^\circ \].
So the correct option is B.

Note:Do not think that at the poles the gravity will be less. You can simply understand this by considering the shape of our earth. As we know, our earth is an oblate shaped one. The distance between the centre point of earth and poles is smaller compared to the equator. It is advised to learn the following equation. So you can find out the answer directly for any latitude problems.
\[{{g}_{\theta }}=g-R{{\omega }^{2}}{{\cos }^{2}}\theta \]
Even though for calculations, we are using acceleration due to gravity as a constant and that is \[9.8m{{s}^{-2}}\]