Question

The difference between two acute angles of a right-angled triangle is $\dfrac{2\pi }{5}$ radians. Express the angles in degrees.

Answer 1

Hint: We will apply the theorem which states that the sum of the interior angle of a triangle is equal to ${{180}^{\circ }}$. We will use the formula which is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$ to solve the question. This can also be written as ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ after dividing the equation by $\pi $.

Complete step-by-step answer:
We will draw a circle showing radians and degrees. The required figure is given below.

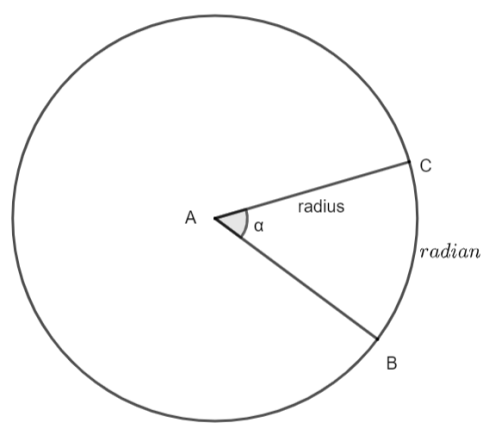
In the diagram AC and AB are the radii of the circle. The radian is an arc which is formed by two radii in a circle joining together at point A. In this figure the radian is represented by an arc BC. The is called an angle made by the two radii intersecting at point A. In the figure the angle is represented by $\angle BAC=\alpha $. Now, the relation between radians and degree is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ after dividing the equation by $\pi $. According to the question we have a right- angled triangle along with two acute angles. Let these angles be A and C as shown below where $\angle A=\alpha $ and $\angle C=\gamma $. Since, it is not given that this right angled triangle is isosceles. Therefore, the acute angles will be of distinct values. That is $\alpha \ne \gamma $.
The figure representing the required right-angled triangle is given below.

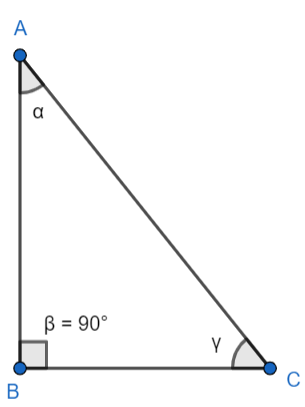
Without losing the generality we consider that $\angle A=\alpha $ is greater than $\angle C=\gamma $. Now, in the question it is given that the difference between two acute angles of a right-angled triangle is $\dfrac{2\pi }{5}$ radians. Therefore, we have
$\begin{align}
  & \angle A-\angle C={{\left( \dfrac{2\pi }{5} \right)}^{c}} \\
 & \Rightarrow \alpha -\gamma ={{\left( \dfrac{2\pi }{5} \right)}^{c}} \\
\end{align}$
Now, we will apply the formula ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ to convert ${{\left( \dfrac{2\pi }{5} \right)}^{c}}$ into its corresponding degree. We can write ${{\left( \dfrac{2\pi }{5} \right)}^{c}}$ as ${{\left( \dfrac{2\pi }{5} \right)}^{c}}=\dfrac{2\pi }{5}\times {{\left( 1 \right)}^{c}}$. After keeping ${{\left( 1 \right)}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ we get
$\begin{align}
  & {{\left( \dfrac{2\pi }{5} \right)}^{c}}=\dfrac{2\pi }{5}\times {{\left( 1 \right)}^{c}} \\
 & \Rightarrow {{\left( \dfrac{2\pi }{5} \right)}^{c}}=\dfrac{2\pi }{5}\times {{\left( \dfrac{180}{\pi } \right)}^{\circ }} \\
 & \Rightarrow {{\left( \dfrac{2\pi }{5} \right)}^{c}}={{\left( \dfrac{2\pi }{5}\times \dfrac{180}{\pi } \right)}^{\circ }} \\
 & \Rightarrow {{\left( \dfrac{2\pi }{5} \right)}^{c}}={{\left( \dfrac{2}{1}\times \dfrac{36}{1} \right)}^{\circ }} \\
 & \Rightarrow {{\left( \dfrac{2\pi }{5} \right)}^{c}}={{\left( 2\times 36 \right)}^{\circ }} \\
 & \Rightarrow {{\left( \dfrac{2\pi }{5} \right)}^{c}}={{\left( 72 \right)}^{\circ }} \\
\end{align}$
Therefore, we have ${{\left( \dfrac{2\pi }{5} \right)}^{c}}={{\left( 72 \right)}^{\circ }}$. As we know that $\alpha -\gamma ={{\left( \dfrac{2\pi }{5} \right)}^{c}}$. Thus, we have $\alpha -\gamma ={{\left( 72 \right)}^{\circ }}...(i)$.
Now, as we know that the sum of the interior angle of a triangle is equal to ${{180}^{\circ }}$. Thus, we can have that
$\begin{align}
  & \angle A+\angle B+\angle C={{180}^{\circ }} \\
 & \Rightarrow \alpha +\beta +\gamma ={{180}^{\circ }} \\
\end{align}$
As we have $\angle B={{90}^{\circ }}$ or, $\beta ={{90}^{\circ }}$. Therefore, we have
$\begin{align}
  & \alpha +\beta +\gamma ={{180}^{\circ }} \\
 & \Rightarrow \alpha +{{90}^{\circ }}+\gamma ={{180}^{\circ }} \\
 & \Rightarrow \alpha +\gamma ={{180}^{\circ }}-{{90}^{\circ }} \\
 & \Rightarrow \alpha +\gamma ={{90}^{\circ }}...(ii) \\
\end{align}$
Now, we will solve equation (i) and (ii). Thus, we get
$\begin{align}
  & \alpha -\gamma ={{72}^{\circ }} \\
 & \underline{\alpha +\gamma ={{90}^{\circ }}} \\
 & 2\alpha +0={{162}^{\circ }} \\
\end{align}$
Solving it further we have $2\alpha ={{162}^{\circ }}$ or, $\alpha ={{81}^{\circ }}$. Now, we will put this value in equation (i). Thus, we get
$\begin{align}
  & {{81}^{\circ }}-\gamma ={{72}^{\circ }} \\
 & \Rightarrow {{81}^{\circ }}-{{72}^{\circ }}=\gamma \\
\end{align}$
Or, ${{9}^{\circ }}=\gamma $.
Hence, the required acute angles $\angle A$, $\angle C$ are $\alpha ={{81}^{\circ }}$ and ${{9}^{\circ }}=\gamma $ respectively.

Note: Alternatively, we could have also considered that $\angle C=\gamma $ is greater than $\angle A=\alpha $. Here these two angles are acute angles and cannot be equal to each other. This is because we have given that the difference between two acute angles of a right-angled triangle is $\dfrac{2\pi }{5}$ radians and by this we have come to know that the two acute angles $\angle A$ and $\angle C$ are not equal.