Question

The difference between the two parallel sides of a trapezium is 8 m. The perpendicular distance between them is 24 m. If the area of the trapezium is $312{{m}^{2}}$, then what are the lengths of the two parallel sides?
(a) 17 m
(b) 18 m
(c) 19 m
(d) 16 m

Answer 1

Hint: Assume the length of parallel sides of the trapezium as a and b in which b is greater than a. Now, form a relation between a and b using the information given about the difference of the sides. For the second relation use the formula $A=\dfrac{h}{2}\left( a+b \right)$ where A is the area of trapezium and h is the distance between the parallel sides. Substitute all the given values and form the second relation between a and b. Solve the two equations to get the values of a and b.

Complete step by step solution:
Here we have been provided with a trapezium with the difference of its parallel sides as 8 m, perpendicular distance between the parallel sides as 24 m and the area as $312{{m}^{2}}$. We have been asked to determine the length of the parallel sides.

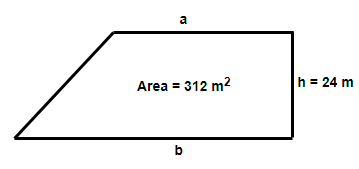
Now, let us assume the length of parallel sides as a and b where side b is greater than a. So, according to the question we have,
$\Rightarrow b-a=8...........\left( i \right)$
We know that the area of a trapezium is given as $A=\dfrac{h}{2}\left( a+b \right)$ where A = area, h = height or distance between the parallel sides. So substituting the values given in the question: h = 24 and area = 312 we get,
$\begin{align}
  & \Rightarrow 312=\dfrac{24}{2}\left( a+b \right) \\
 & \Rightarrow 312=12\left( a+b \right) \\
 & \Rightarrow \left( a+b \right)=26..........\left( ii \right) \\
\end{align}$
Solving equations (i) and (ii) we get,
$\Rightarrow a=9$ and $b=17$
Therefore the length of the shorter side is 9 m and the length of the longer side is 17 m. hence option (a) is the correct answer.

Note: In the options you may note that we have the length of only one side. However, we have solved for both the sides because we didn’t know initially which of the sides a or b is provided in the option. You must remember the formula of the area of a trapezium otherwise it will be difficult to form the second relation.