Question

The difference between the two acute angles of a right angle triangle is \[\dfrac{2\pi }{5}\] radians. Express the angles in degrees.

Answer 1

Hint: We know that a right angled triangle is a triangle in which one angle measures \[{{90}^{\circ }}\]. We will use the properties of a triangle that the sum of all interior angles of a triangle is equal to \[{{180}^{\circ }}\]. Also, we will use the conversion of radians into degree as follows:
1 radian \[=\dfrac{180}{\pi }\] degree

Complete step-by-step answer:

Let us suppose a right angled triangle \[\Delta ABC\] right angled at C.

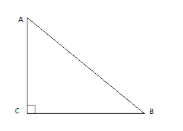
\[\Rightarrow \angle ACB={{90}^{\circ }}\]
We have been given that the difference between two acute angles is \[\dfrac{2\pi }{5}\] radians.
\[\Rightarrow \angle CAB-\angle CBA=\dfrac{2\pi }{5}\] radians.
We know that 1 radian \[=\dfrac{180}{\pi }\] degree
So, \[\dfrac{2\pi }{5}\] radians are equal to:
\[\begin{align}
  & =\dfrac{180}{\pi }\times \dfrac{2\pi }{5}degree \\
 & =\dfrac{360}{5}degree \\
 & =72degree \\
\end{align}\]
\[\begin{align}
  & \Rightarrow \angle CAB-\angle CBA=72degree \\
 & \Rightarrow \angle CAB-\angle CBA={{72}^{\circ }}.....(1) \\
\end{align}\]
Also, we know that the sum of interior angles of a triangle is equal to \[{{180}^{\circ }}\].
Since \[\Delta ABC\] is right angled triangle at C
\[\begin{align}
  & \Rightarrow \angle ACB={{90}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}+\angle CAB+\angle CBA={{180}^{\circ }} \\
\end{align}\]
On taking \[{{90}^{\circ }}\] to the right hand side, we get:
\[\begin{align}
  & \Rightarrow \angle CAB+\angle CBA={{180}^{\circ }}-{{90}^{\circ }} \\
 & \Rightarrow \angle CAB+\angle CBA={{90}^{\circ }}.....(2) \\
\end{align}\]
On adding (1) and (2) we get as follows:
\[\begin{align}
  & \angle CAB-\angle CBA+\angle CBA+\angle CAB={{72}^{\circ }}+{{90}^{\circ }} \\
 & \Rightarrow 2\angle CAB={{162}^{\circ }} \\
 & \Rightarrow \angle CAB={{81}^{\circ }} \\
\end{align}\]
On substituting the value of \[\angle CAB\] in equation (1) we get as follows:
\[{{81}^{\circ }}-\angle CBA={{72}^{\circ }}\]
On taking \[{{72}^{\circ }}\] to the left hand side, we get as follows:
\[\begin{align}
  & {{81}^{\circ }}-{{72}^{\circ }}=\angle CBA \\
 & {{9}^{\circ }}=\angle CBA \\
\end{align}\]
Therefore, the angles in degrees are \[{{9}^{\circ }},{{81}^{\circ }},{{90}^{\circ }}\].

Note: Be careful while doing calculation of conversion of radians into degrees. Take care of the sign while solving the equations. Remember that 1 radian \[=\dfrac{180}{\pi }\] degree instead of this don’t use 1 radian \[=\dfrac{\pi }{180}\] degree by mistake.