Question

The difference between the radii of the smaller circle and the bigger circle is 7 cm and the difference between the areas of the two circles is 1078 sq cm. What is the radius of the smaller circle in cm?
(a) 28
(b) 21
(c) 17.5
(d) 35

Answer 1

Hint: We will assume the radius of the smaller circle as r and the radius of the bigger circle as r+7 because the difference between their radius is 7. Also the difference between their areas is mentioned and for calculating the areas we will use the formula \[\pi {{r}^{2}}\].

Complete step-by-step answer:
It is mentioned in the question that the difference between the radii of the smaller circle and the bigger circle is 7 cm. So let the radius of the smaller circle be r and hence the radius of the bigger circle will be r+7. So the figure is,

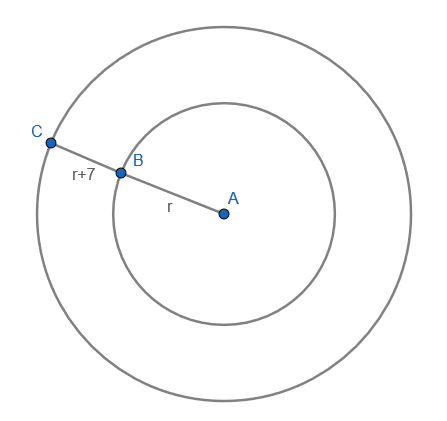
Now, area of the smaller circle \[=\pi {{r}^{2}}......(1)\]
Area of the bigger circle \[=\pi {{(r+7)}^{2}}......(2)\]
Now it is also mentioned in the question that the difference between the areas of the bigger circle and smaller circle is 1078 sq. cm. So using this information we subtract equation (2) and equation (1) and then we equate it to 1078. Doing this we get,
\[\Rightarrow \pi {{(r+7)}^{2}}-\pi {{r}^{2}}=1078........(3)\]
Now first taking common terms out and then expanding the squares in equation (3) we get,
\[\Rightarrow \pi \left[ {{r}^{2}}+49+14r-{{r}^{2}} \right]=1078........(4)\]
Now cancelling similar terms in equation (4) we get,
\[\Rightarrow \pi \left[ 49+14r \right]=1078........(5)\]
Now rearranging and simplifying equation (5) we get,
\[\Rightarrow 49+14r=\dfrac{1078\times 7}{22}........(6)\]
Now solving for r in equation (6) we get,
\[\begin{align}
  & \Rightarrow 49+14r=343 \\
 & \Rightarrow 14r=294 \\
 & \Rightarrow r=\dfrac{294}{14}=21 \\
\end{align}\]
So the radius of the smaller circle is 21 cm. Hence the correct answer is option (b).

Note: Remembering the formula of the area \[\pi {{r}^{2}}\] is the key here. Also when we draw the figure from the given details in the question things become very much clear. We in a hurry can make a mistake in solving equation (3) as we may expand \[{{(r+7)}^{2}}\] incorrectly and hence we need to be careful while doing this calculation.