Question

The difference between the outer and inner curved surface area of hollow right circular cylinder 14cm long is 88$cm^2$. If the volume of metal used in making the cylinder is 176$cm^3$, find the outer and inner diameters of the cylinder. (Use $\pi =\dfrac{22}{7}$)

Answer 1

Hint: The difference between the outer and inner curved surface area of hollow right circular cylinder 14cm long is 88$cm^2$, using this we make our equation number one. Similarly, the difference of volume of inner and outer part of hollow right circular cylinder is also given, using this we make another equation named as equation number two. By adding both the equations, we get one of the diameters and putting the value of one of the diameters, we also get the value of another diameter.

Complete Step-by-step answer:

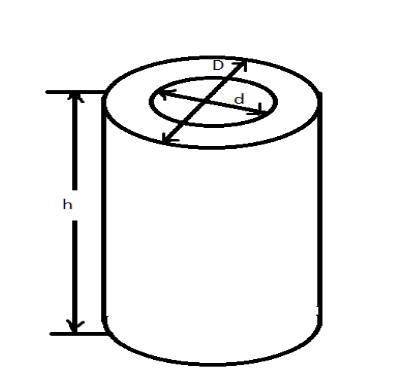
The difference of outer curved surface area and inner curved surface area is 88$cm^2$ given in the question.
So,
Outer curved surface area – Inner curved surface area $=88c{{m}^{2}}$.
Since, the curved surface area of a cylinder is $2\pi rh$, where r is the radius and h is the height of the cylinder.
In our problem, the height of the cylinder is 14 cm.
$\begin{align}
  & 2\pi Rh-2\pi rh=88 \\
 & 2\pi h(R-r)=88 \\
 & R-r=\dfrac{88}{2\times \dfrac{22}{7}\times 14} \\
 & R-r=\dfrac{88\times 7}{2\times 22\times 14} \\
 & R-r=1...(1) \\
\end{align}$
Also, the difference of volume of outer part and inner part of cylinder is given.
So, Volume of outer part – Volume of inner part$=176$.
Since, the volume of a cylinder is $\pi {{r}^{2}}h$, where r is the radius and h is the height of the cylinder.

$\begin{align}
  & \pi {{R}^{2}}h-\pi {{r}^{2}}h=176 \\
 & \pi h\left( {{R}^{2}}-{{r}^{2}} \right)=176 \\
\end{align}$
We expand the $({{R}^{2}}-{{r}^{2}})$ using the identity $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)$.
$\begin{align}
  & \pi h\left( R-r \right)\left( R+r \right)=176 \\
 & \pi \times 14\left( R+r \right)=176 \\
 & R+r=\dfrac{176\times 7}{22\times 14} \\
 & R+r=4...(2) \\
\end{align}$
Adding equation (1) and equation (2), we get
$\begin{align}
  & R+r+R-r=5 \\
 & 2R=5 \\
 & R=\dfrac{5}{2} \\
 & D=5 \\
\end{align}$
Putting in equation (2),
$\begin{align}
  & \dfrac{5}{2}+r=4 \\
 & r=4-\dfrac{5}{2} \\
 & r=\dfrac{8-5}{2} \\
 & r=\dfrac{3}{2} \\
 & d=3. \\
\end{align}$
Hence, the diameter of outer cylinder is 5cm and the diameter of inner cylinder is 3cm.

Note: The key step for solving this problem is assuming the radius of outer and inner cylinders as a variable and then establishing the desired relationship between these variables by using the surface area and volume portion given for the cylinder. After this, only the mathematical part is left for obtaining the final answer.