Question

The difference between the length and breadth of a rectangle is 23m. If its perimeter is 206m, then its area is:
(a) $1520{{m}^{2}}$
(b) $2420{{m}^{2}}$
(c) $2480{{m}^{2}}$
(d) $2520{{m}^{2}}$

Answer 1

Hint: Assume that the length of the rectangle is ‘x’. Write the breadth of the rectangle in terms of ‘x’ based on the data given in the question. Write a linear equation in ‘x’ using the fact that the perimeter of the rectangle is $2\left( l+b \right)$, where ‘l’ is the length of the rectangle and ‘b’ is the breadth of the rectangle. Simplify the equation to calculate the length and breadth of the rectangle. Calculate the area of the rectangle by multiplying length and breadth.

Complete step-by-step answer:

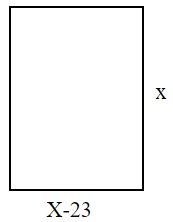
We know that the difference between length and breadth of a rectangle is 23m and its perimeter is 206m. We have to calculate the area of the rectangle.
Let’s assume that the length of the rectangle is ‘x’. As the difference between length and breadth is 23m, the breadth of the rectangle is $x-23$.
We know that the perimeter of the rectangle is given by $2\left( l+b \right)$, where ‘l’ is the length of the rectangle and ‘b’ is the breadth of the rectangle.
Substituting $l=x,b=x-23$ in the above expression, the perimeter of the rectangle is $2\left( x+x-23 \right)$.
We know that the perimeter of the rectangle is 206m.
Thus, we have $2\left( x+x-23 \right)=206$.
Simplifying the above equation, we have $2x-23=\dfrac{206}{2}=103$.
Rearranging the terms of the above equation, we have $2x=103+23=126$.
Thus, we have $x=\dfrac{126}{2}=63m$.
Substituting $x=63m$ in the expression $x-23$, the breadth of the rectangle is $=x-23=63-23=40m$.
Thus, the length and breadth of the rectangle are 63m and 40m respectively.

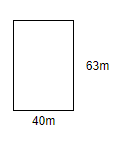
We will now calculate the area of the rectangle. We know that the area of the rectangle is the product of the length and breadth of the rectangle.
Thus, the area of the rectangle $=63\times 40=2520{{m}^{2}}$.
Hence, the area of the given rectangle is $2520{{m}^{2}}$, which is option (d).

Note: We can also solve this question by assuming that the breadth of the rectangle is ‘x’ and writing length in terms of ‘x’. One must be careful about units while calculating the area of the rectangle. As the perimeter is in metres, the length of sides is in metres and thus, the area is in metres square.