Question

The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find
(i)The area of the metal sheet used to make the bucket?
(ii)Why we should avoid the bucket made by ordinary plastic (use \[\pi =3.14\])

Answer 1

Hint: To start with, in the given problem we are dealing with a cone where we are to find the total surface area of the cone. The total area of the cone consists of the area of the curved surface area and the area of the base. So, we will solve the slant height of the cone and total surface area based on the given data and finally we solve the second solution.

Complete step-by-step solution:
According to the question, we are given the diameters of the lower and upper ends of a bucket in the form of a frustum of a cone.
Height of the cone\[\left( h \right)=24cm\]
Radius of lower end of the bucket \[\left( {{r}_{1}} \right)=\dfrac{10}{2}=5cm\]
Radius of upper end of the bucket \[\left( {{r}_{2}} \right)=\dfrac{30}{2}=15cm\]

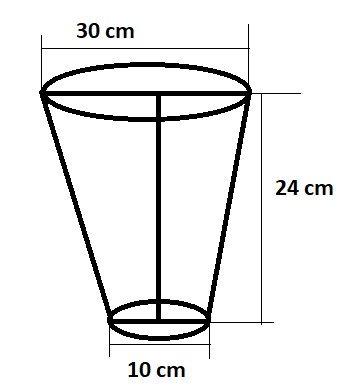
Here, in this cone, we need to find out the slant height of the cone.
Slant height \[\left( l \right)=\sqrt{{{h}^{2}}+{{\left( {{r}_{2}}-{{r}_{1}} \right)}^{2}}}\]
Here we do not consider the top part area of frustum as this will be open from the top.
Substituting the values of \[h,{{r}_{1}},{{r}_{2}}\]
\[\Rightarrow \sqrt{{{\left( 24 \right)}^{2}}+{{\left( 15-5 \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{\left( 24 \right)}^{2}}+{{\left( 10 \right)}^{2}}}\]
On further evaluation,
\[\Rightarrow \sqrt{576+100}=\sqrt{676}=26cm\]
Now, area of the metal sheet used to make the bucket= total surface is of the bucket (excluding the upper end)
Total Surface Area\[\left( TSA \right)=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi {{r}_{1}}^{2}\]
 On substituting the values of terms required in the TSA formula, we get
\[\Rightarrow \left( 3.14 \right)\left( 15+5 \right)\left( 26 \right)+\left( 3.14 \right){{\left( 5 \right)}^{2}}\]
On further solving, we get
\[\Rightarrow 1632.8+78.5=1711.3c{{m}^{2}}\]
 Area of the metal sheet used to make the bucket is \[1711.3c{{m}^{2}}\].
(ii) We should avoid the bucket made of ordinary plastic as plastic is hazardous and non-biodegradable to the environment.

Note: In the given problem, we are dealing with the area of the cone. A cone is a shape formed by using a set of line segments or the lines which connects a common point, called the apex or vertex, to all the points of a circular base (which doesn’t contain the apex). The distance from the vertex of the cone to the base is the height of the cone. The circular base has a measured value of radius. And the length of the cone from apex to any point on the circumference of the base is the slant height.