Question

The diameter of the front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that the rear wheel will make in covering distance in which the front wheel makes 1400 revolutions.

Answer 1

Hint: First use the formula \[D=\left( 2\times \pi \times r \right)\times n\] to find the distance covered by the front wheel and then equate it with the formula of distance travelled by real wheel to get the answer.

Complete step-by-step answer:

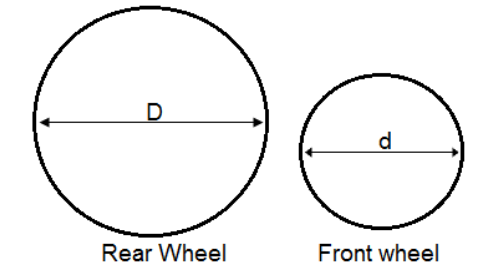
To solve the above problem we will write the given data first and assume some variables to them,
Diameter of front wheel = d = 80 cm = \[80\times {{10}^{-2}}\]m = 0.8 m
Therefore radius of front wheel = r = \[\dfrac{d}{2}\] = \[\dfrac{0.8}{2}\] = 0.4 m …………………………………. (1)
Number of revolutions of the front wheel = n = 1400 …………………………………………………. (2)
Diameter of rear wheel = D = 2 m
Therefore radius of rear wheel = \[\dfrac{D}{2}\] = \[\dfrac{2}{2}\] = 1 m. …………………………………………….. (3)
Number of revolutions made by rear wheel = N =?

Now to calculate the number of revolutions performed by the rear wheel, first we have to calculate the distance covered by the front wheel as the distance covered by both the wheels is the same.
To calculate the distance covered by the front wheel we should know the formula given below,
Formula:
Distance covered by a circular wheel = Circumference of the circular wheel \[\times \] Number of revolutions
If we consider radius as ‘r’ and number of revolutions as ‘N’ and distance covered as ‘D’ then the above formula can be converted as,
\[D=\left( 2\times \pi \times r \right)\times n\] ……………………………………………….. (3)
If we put the values of equation (1) and equation (2) in the above equation we will get,
\[\therefore D=\left( 2\times 3.142\times 0.4 \right)\times 1400\]
\[\therefore D=\left( 6.284\times 0.4 \right)\times 1400\]
\[\therefore D=2.5136\times 1400\]
\[\therefore D=3519.04\] …………………………………………………….. (4)
As we know that the distance covered by both the wheels is the same, therefore the distance covered by the rear wheel will also become ‘D’.
If we put the distance as D, radius as ‘R’ and number of revolutions as ‘N’ in equation we will get the formula for distance covered by rear wheel as follows,
\[\therefore D=\left( 2\times \pi \times R \right)\times N\]
\[\therefore 3519.04=\left( 2\times 3.142\times 1 \right)\times N\]
\[\therefore \left( 2\times 3.142\times 1 \right)\times N=3519.04\]
\[\therefore \left( 6.284 \right)\times N=3519.04\]
\[\therefore N=\dfrac{3519.04}{\left( 6.284 \right)}\]
Therefore, N = 560
Therefore the number of revolutions performed by the rear wheel is 560.

Note: We can solve this problem without substituting the value of \[2\pi \] because it is going to be cancelled while equation with same formula for rear wheel i.e. \[\therefore D=\left( 2\times \pi \times R \right)\times N\]