Question

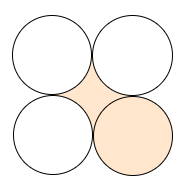
The diameter of all the four circles is 7 cm. The circles are touching each other at only one point as shown in the figure. What is the area of the shaded portion in the figure?

A. 49 sq. cm
B. 38.5 sq. cm
C. 22 sq. cm
D. cannot be determined

Answer 1

Hint: We will first find the area flanked by the four circles by joining the centres of the circles. Then we will subtract the area of the sum of the four quadrants from the square. We will then find the area of one of the circles and add them. While finding the area, we will use the formula for finding the area of the quadrant, which is given by, $\dfrac{\pi {{r}^{2}}}{4}$, area of circle as $\pi {{r}^{2}}$ and area of square as ${{l}^{2}}$, where r is the radius and l is the side length of the square.

Complete step-by-step answer:
In the question, we have been given a figure and are asked to find the area of the shaded portion in the figure. The figure is as below,

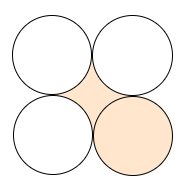
We know that the diameter of the given circles are 7 cm, so its radius would be $\dfrac{7}{2}$ cm or 3.5 cm. The shaded portions are one of the four circles and an area flanked by all the four circles. So, we will first find the area of the portion flanked by the four circles, whose radius is 3.5 cm. This can be represented in the figure below.

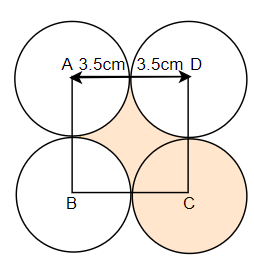
So, as we can see we have joined the centres of the circles to get a square ABCD. So, we will find the area of the square ABCD and then subtract the area of the four quadrants that are present in the square. We will then get the area of the shaded portion.
As we know that the radius of the circle is 3.5 cm and that the side length of the square is twice the radius, so the length of the square would be $2\times 3.5$ or 7 cm. We know that the area of the quadrant is given by, $\dfrac{\pi {{r}^{2}}}{4}$, where r is the radius of the circle. SO, here, r or radius is 3.5 cm, so the area of the quadrant would be, $\dfrac{\pi \times {{\left( 3.5 \right)}^{2}}}{4}$. We know the value of $\pi =\dfrac{22}{7}$, so we get the area of the quadrant as,
$\begin{align}
  & \dfrac{1}{4}\times \dfrac{22}{7}\times 3.5\times 3.5 \\
 & \Rightarrow \dfrac{38.5}{4}c{{m}^{2}} \\
\end{align}$
We know that there are 4 quadrants, thus the total area of the quadrants would be 4 times the area of 1 quadrant, which is,
$\begin{align}
  & 4\times \dfrac{38.5}{4}c{{m}^{2}} \\
 & \Rightarrow 38.5c{{m}^{2}} \\
\end{align}$
We will now find the area of the square. We know that the side length of the square is 7 cm, so its area will be,
${{l}^{2}}\Rightarrow {{\left( 7 \right)}^{2}}=49c{{m}^{2}}$
So, the area of the shaded portion will be, ( Area of square - total area of quadrants), which is,
$\left( 49-38.5 \right)c{{m}^{2}}=10.5c{{m}^{2}}$
Now, we will find the area of the one circle that is shaded in the given figure. The radius of the circle is given as 3.5 cm, so area of the circle would be,
$\begin{align}
  & \pi {{r}^{2}} \\
 & \Rightarrow \dfrac{22}{7}\times {{\left( 3.5 \right)}^{2}} \\
 & \Rightarrow 38.5c{{m}^{2}} \\
\end{align}$
So, the total area of the shaded portion is given by,
$\left( 38.5+10.5 \right)c{{m}^{2}}=49c{{m}^{2}}$

So, the correct answer is “Option A”.

Note: We know that four quadrants constitute a full circle, so instead of calculating each quadrant by using the formula of $\dfrac{\pi {{r}^{2}}}{4}$ and then adding them, we can simply find the area of one circle using the formula $\pi {{r}^{2}}$, where r is the radius. This will help us save time and solve the question with fewer steps.