Question

The diameter of a wheel is 1.26 meter. How far will it travel in 500 revolutions?
A.1980 meters
B.2000 meters
C.2420 meters
D.1890 meters

Answer 1

Hint:To solve this question, firstly we need to know the meanings of a few terms.
Diameter: A diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle.
Radius: A radius is a straight line from the center of a circle to the edge of the circle.
Circumference: Circumference is the distance around the edge of a circle. In other words, it is the perimeter of the circle.

Complete Step-by-step answer:
For this question, firstly we need to find the radius of this wheel. To find the radius of the circle, we need to divide the diameter of the circle by 2. So, to find the radius of the wheel, we will divide 1.26 meter by 2. Now, we need to find the circumference of this wheel. The formula that is used to find the circumference or the perimeter of the circle is \[2\pi r\] . In this formula, the value of the symbol \[\pi \]
 Is \[\dfrac{22}{7}\] . And the letter ‘r’ refers to the radius of the circle. So, the formula to find the circumference of the circle is ‘\[2\times \dfrac{22}{7}\times \] radius of the circle’.

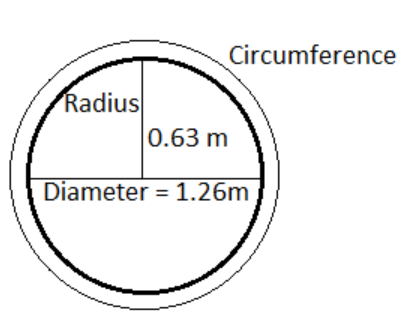
The Diameter of the wheel = 1.26 meter
Radius of the wheel = \[\dfrac{1.26}{2}\] meter = 0.63 meter
Circumference of the wheel = \[2\pi r\] = ( \[2\times \dfrac{22}{7}\times 0.63\] ) meter
                                                                           = 3.96 meter

Total number of revolutions = 500
Distance traveled in 500 revolutions = Circumference x 500
                                                                            = 3.96 x 500 = 1980 meters
So, the answer is (a) 1980 meters.

Note:The value of “pi” is always constant, i.e., its value always remains \[\dfrac{22}{7}\]. The students can make a mistake by not paying attention to the fact that in the question the diameter has been given rather than the radius of the circle.