Question

The diameter of a sphere is decreased by 25%. Find the percentage of decrease of its curved surface area?

Answer 1

Hint: We start solving the given question by finding the curved surface area of original sphere using the formula $Curved\text{ }Surface\text{ }Area=4\pi \times {{\left( radius \right)}^{2}}$. Then we decrease the diameter by 25% and find the curved surface area of the new sphere formed and then we find the percentage of decrease of the curved surface area from original sphere to new sphere.

Complete step-by-step answer:
Let us consider the radius of the sphere as $r$, and let its diameter be $d$ and let its curved surface area be $C$.

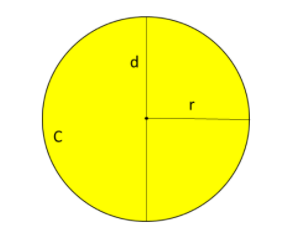
Let us use the formula for the diameter of sphere,
$diameter=2\times radius$
Then, the diameter of our given sphere in terms of radius is given by $d=2r$.
Using the formula for the curved surface area of the sphere,
$Curved\text{ }Surface\text{ }Area=4\pi \times {{\left( radius \right)}^{2}}$
Applying the above formula, we get
$C=4\pi {{r}^{2}}$
Given that the diameter of the curve is decreased by 25%.
Let the new diameter be ${d}'$ and radius be ${r}'$ and curved surface area be ${C}'$.
Then we can write ${d}'$ in terms of $d$ as
$\begin{align}
  & \Rightarrow {d}'=d-\left( \dfrac{25}{100}\times d \right) \\
 & \Rightarrow {d}'=d-\left( \dfrac{d}{4} \right) \\
 & \Rightarrow {d}'=\dfrac{3d}{4}............\left( 1 \right) \\
\end{align}$
Then as $d=2r$ and ${d}'=2{r}'$, by substituting them in equation (1) we get,
$\begin{align}
  & \Rightarrow 2{r}'=\dfrac{3\times 2r}{4} \\
 & \Rightarrow {r}'=\dfrac{3\times 2r}{2\times 4} \\
 & \Rightarrow {r}'=\dfrac{3r}{4} \\
\end{align}$
Applying the formula for the curved surface area of the sphere again, we get the Curved Surface Area of new sphere as
$\begin{align}
  & \Rightarrow {C}'=4\pi {{{{r}'}}^{2}} \\
 & \Rightarrow {C}'=4\pi {{\left( \dfrac{3r}{4} \right)}^{2}} \\
 & \Rightarrow {C}'=4\pi \times \dfrac{9{{r}^{2}}}{16} \\
 & \Rightarrow {C}'=\dfrac{9\pi {{r}^{2}}}{4} \\
\end{align}$
So, now we can find the percentage of decrease of curved surface area as
$\begin{align}
  & =\dfrac{C-{C}'}{C}\times 100 \\
 & =\dfrac{4\pi {{r}^{2}}-\dfrac{9\pi {{r}^{2}}}{4}}{4\pi {{r}^{2}}}\times 100 \\
 & =\dfrac{\dfrac{16\pi {{r}^{2}}-9\pi {{r}^{2}}}{4}}{4\pi {{r}^{2}}}\times 100 \\
\end{align}$
$\begin{align}
  & =\dfrac{\dfrac{7\pi {{r}^{2}}}{4}}{4\pi {{r}^{2}}}\times 100 \\
 & =\dfrac{7\pi {{r}^{2}}}{4\times 4\pi {{r}^{2}}}\times 100 \\
 & =\dfrac{7}{16}\times 100 \\
 & =43.75\% \\
\end{align}$
Hence, we get that the decrease in the curved surface area is equal to 43.75%.
Hence, the answer is 43.75%.

Note: One can make a mistake while solving the problem by substituting the diameter of the new sphere in the formula of curved surface area of sphere instead of using radius of the new sphere.