Question

The diameter of a metallic ball is 4.2 cm What is the mass of the ball, if the density of the metal is 8.9 cm³ ?

Answer 1

Hint: We will use the following formulas and substitute the given values and calculate that of the unknown.
Density = Mass/volume
Diameter = 2 x Radius

Complete step-by-step answer:

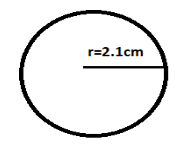
Calculating volume of ball : (To substitute in that of density)
Diameter = 4.2 cm (given)
Radius = 4.2/2 =2.1 cm (∴ R= D/2)
Now,
Volume of sphere = $4/3\pi {r^3}$
Substituting the value of r
\[4/3\pi {r^3} = (4/3)\times(22/7)\times{(2.1)^3}\]
\[
   = (4/3)\times(22/7)\times2.1\times2.1\times2.1 \\
   = (4/3)\times(22/7)\times(21/10)\times(21/10)\times(21/10) \\
 \]
(To remove decimal and make calculation easier)
\[ = 38808/1000\]
\[ = 38.808\] cm³
Now, Density= Mass/ Volume = 8.9 (given)
\[8.9 = M/38.808\]
Calculating Mass:
\[M = 8.9\times38.808\]
\[ = 345.3912\] g
Therefore the mass of the metallic ball is 345.3912 g.

Note: As the given density is in g/cm3, volume has to be in cm³, and the mass is calculated in grams. The mean curvature, width and circumference are constant of a sphere. All the points present on the surface are equidistant from the centre.