Question

The diameter of a garden roller is 1.4 m and it is 2 m long. How much area will it cover in one revolution?
(a) \[6.8\,{{m}^{2}}\]
(b) \[8.8\,{{m}^{2}}\]
(c) \[3.8\,{{m}^{2}}\]
(d) \[5.8\,{{m}^{2}}\]

Answer 1

Hint: The garden roller is in the shape of a right circular cylinder. To find the area that the garden roller covers in one revolution, we need to find the lateral area of the garden roller. The lateral area of the garden roller is equal to the area of its curved surface.

Complete step-by-step answer:
We will first draw the diagram from the details mentioned in the question.

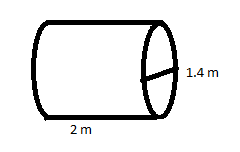
The formula for finding the lateral area of a right circular cylinder is: \[\text{L=}2\pi rh......(1)\] where L is the lateral surface area of the cylinder, r is the radius of the cylinder and h is the cylinder’s height.
Since the garden roller is positioned horizontal as it rolls along the ground, then the length of the roller is actually its height.
Now in the question diameter is mentioned and we need to find a radius which is half of diameter.
Diameter of the garden roller \[=d=1.4\,m\]
Radius of the garden roller \[=r=\dfrac{d}{2}=\dfrac{1.4}{2}=0.7\,m\]
Height of the garden roller \[=h=2\,m\]

Now putting value of r and h in equation (1) to get the lateral area of the garden roller we get,
 \[\text{L=}2\times \dfrac{22}{7}\times 0.7\times 2=8.8\,{{m}^{2}}......(2)\]
 \[\text{A}=\text{n }\!\!\times\!\!\text{ L}.....(3)\] where A is the area covered by the roller, n is the number of revolutions and L is the lateral area of the roller.
In the question the given number of revolutions is 1 that is \[\text{n}=1\]. Now substituting this value of n and the value of L from equation (2) in equation (3) we get,
 \[\text{A}=1\text{ }\!\!\times\!\!\text{ 8}\text{.8=8}\text{.8 }{{m}^{2}}\]
Hence the area covered by the garden roller in one revolution is \[\text{8}\text{.8 }{{m}^{2}}\]. So the correct answer is option (b).

Note: The key here is to understand that the garden roller is nothing but a cylinder. Knowing the formula of lateral area is important and radius is always half of the diameter. We in a hurry may substitute diameter which is 1.4 m in place of radius which is 0.7 m. We need to be careful with the units too because if a unit is missing some marks would be deducted by the examiner.