Question

The diameter of a circle circumscribing a square is $15\sqrt 2 cm$ . What is the length of the side of the square?
A. 15 cm
B. 12 cm
C. 10 cm
D. 7.5 cm

Answer 1

Hint:First, we need to know what is circumscribing and inscribing. A polygon is circumscribed by a circle, if the vertices of the polygon are on the circle. A polygon is inscribed by a circle, if the sides of the polygon are tangents to the circle. We will use the theorem that an angle in a semicircle is a right angle. The inverse is also true.

Complete step by step answer:
First, we will draw a neat diagram which clearly depicts the given question.

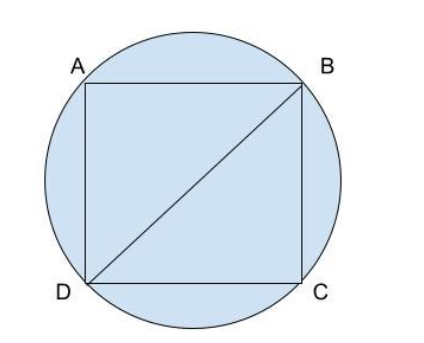
The square ABCD is inscribed inside a circle. The diameter of the circle is $15\sqrt 2 cm$
We know that an angle inside a semicircle is a right angle. Let us consider the length of the side of the square to be $x$ cm. Since, the angle $\angle BCD$ is a right angle, the side BD is the diagonal. If we consider the triangle BCD, the side BD becomes the hypotenuse.

So, BD is the hypotenuse and the diameter of the circle.
$B{C^2} + C{D^2} = B{D^2}$
By substituting the values and variables, we get:
\[{x^2} + {x^2} = {(15\sqrt 2 )^2}\]
On further simplification, we get:
$2{x^2} = 2 \times {15^2}$
Hence, we get that $x = 15$
We only take the positive value since the length of the side can only be positive.Hence, the length of the side is 15cm.

Therefore, the right answer is option A.

Note:In this question, we need to remember the theorem that states that an angle in a semicircle is a right angle. After that, we have to form a correct equation and then solving it will give our answer. We should avoid calculation mistakes and read the question properly to know whether the square is circumscribed by the circle or the polygon circumscribes the circle. A small misconception may change the entire answer.