Question

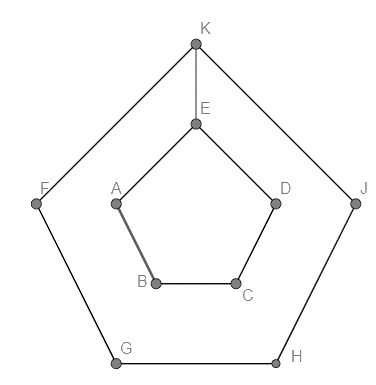
The diagram shows two regular pentagons FGHJK is enlargement of Pentagon ABCDE. The center of both the polygons is O. Find the value of $\angle AEK$

Answer 1

Hint: We know that the angles of regular polygon are equal to ${{108}^{\circ }}$and the sum of all angles that form a rotation is ${{360}^{\circ }}$ . Now also since the polygons are similar we can say that $\angle AEK=\angle DEK$ . Hence we can easily find the value of $\angle AEK$

Complete step-by-step answer:
Now let us first understand the term polygon.
Polygon is any n sided closed figure formed with straight lines.
Now to satisfy the condition that a polygon is always closed we need n to be more than 3.
Hence the smallest polygon is a triangle.
Now if we have n = 4 then the polygon is a quadrilateral.
Similarly if n = 5 then the polygon is called pentagon.
Now let us understand regular polygons.
Regular polygons are polygons with all sides and angles equal.
Hence if any of the side or angle is not equal we would get an irregular polygon.
Let us see some examples of regular polygons.
Regular polygon with three sides is an equilateral triangle.
Regular polygon with 4 sides is a square.
Now consider a regular pentagon.
Now we know that each angle of a regular pentagon is ${{108}^{\circ }}$ .
Consider the given figure.

Here we know that ABCDE is a regular polygon. Hence we can say that AED is equal to ${{108}^{\circ }}$
Now since we have ABCDE and FGHJK are similar then we can say that $\angle AEK=\angle DEK$ .
Let $\angle AEK=\angle DEK=x$
Now we know that $\angle AEK+\angle DEK+\angle AED={{360}^{\circ }}$ since the angles form a rotation.
Substituting the values we get $x+x+{{108}^{\circ }}={{360}^{\circ }}$
\[\begin{align}
  & \Rightarrow 2x={{360}^{\circ }}-{{108}^{\circ }} \\
 & \Rightarrow 2x={{252}^{\circ }} \\
 & \Rightarrow x={{126}^{\circ }} \\
\end{align}\]
Hence we get $\angle AEK={{126}^{\circ }}$

Note: Note that for any regular polygon with n sides each interior angle is given by \[{{180}^{\circ }}-\dfrac{{{360}^{\circ }}}{n}\] for example if we substitute 3 we get \[{{180}^{\circ }}-\dfrac{{{360}^{\circ }}}{3}={{180}^{\circ }}-{{120}^{\circ }}={{60}^{\circ }}\] . Similarly for n = 5 we have \[{{180}^{\circ }}-\dfrac{{{360}^{\circ }}}{5}={{180}^{\circ }}-{{72}^{\circ }}={{108}^{\circ }}\] .