Question

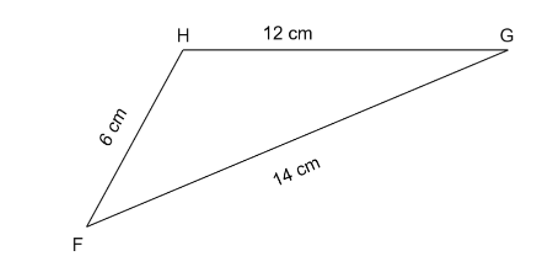
The diagram shows triangle \[FGH\] , with \[FG = 14{\text{ }}cm\] , \[GH = 12{\text{ }}cm\] and \[FH = 6{\text{ }}cm\] . Calculate the size of angle \[HFG\].

Answer 1

Hint: We have to find the value of the angle \[HFG\] . We solve this question using the concept of cosine law of trigonometry and using the values of trigonometric functions . We can find the values of angles of the triangle by applying cosine law . And thereafter finding the value of angle \[HFG\] by putting the values in the formula of cosine law .

Complete step-by-step answer:
All the trigonometric functions are classified into two categories or types as either sine function or cosine function . All the functions which lie in the category of sine functions are sin , cosec and tan functions on the other hand the functions which lie in the category of cosine functions are cos , sec and cot functions . The trigonometric functions are classified into these two categories on the basis of their property which is stated as : when the value of angle is substituted by the negative value of the angle then we get the negative value for the functions in the sine family and a positive value for the functions in the cosine family .
Given :
\[FG = 14{\text{ }}cm\] , \[GH = 12{\text{ }}cm\] and \[FH = 6{\text{ }}cm\]
Let the angles be stated as \[angle{\text{ }}F = angle{\text{ }}HFG\] , \[angle{\text{ }}H = angle{\text{ }}FHG\] and \[angle{\text{ }}G = angle{\text{ }}HGF\] .
We know ,
Formula of cosine law is given as :
\[\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\]
Now , after putting the values we will get the value for \[angle{\text{ }}C\]
Putting the values for the formula , we get
\[\cos F = \dfrac{{{{(FH)}^2} + {{(FG)}^2} - {{(HG)}^2}}}{{2 \times FH \times FG}}\]
Putting the values in the formula , we get
After solving we get ,
\[\cos F = \dfrac{{{6^2} + {{14}^2} - {{12}^2}}}{{2 \times 6 \times 14}}\]
On further simplifying , we get
\[\cos F = \dfrac{{36 + 196 - 144}}{{2 \times 6 \times 14}}\]
We get ,
\[\cos F = \dfrac{{88}}{{168}}\]
After further simplifying , we get
\[\cos F = \dfrac{{11}}{{21}}\]
Taking \[{\cos ^{ - 1}}\] both sides , we get
As , \[{\cos ^{ - 1}}[\cos x] = x\]
Then ,
\[F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]\]
Thus the value of angle \[HFG\] is \[F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]\] .
So, the correct answer is “\[F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]\]”.

Note: The formula of triangle law of sine is given as :
\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}\]
The formula of triangle law of cosine is given as :
\[\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\]
Where \[A\] , \[B\] , \[C\] are the angles of the triangle \[ABC\] and \[a\] , \[b\] , \[c\] are the sides of the triangle \[ABC\].
These formulas must be remembered. Calculations must be verified to be sure of the answer.