Question

The diagram shows the inner boundary of a $600$ metre running track which has two parallel straight lines each of length $200$ metres and two semi-circular ends. Calculate the radius of each semi-circular end.

Answer 1

Hint: If we need to answer these types of questions, then we need to be clear with the language. In the question, we are given a word problem in which we are provided with the circumference of a running track made of two straight parallel lines and two semi-circular ends. So, we have to calculate the radius of both the semi-circular ends provided the lengths of the straight parallel lines. We must know how to calculate the perimeter of such fused shapes in order to solve the problem. Then, we substitute the values of two sides of the rectangle known to us and solve for the radius of the semicircles.

Complete step by step answer:
So, the length of the straight parallel lines is $200$ metres. The total length of the running track is $600$ metres.

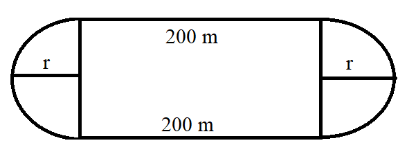
Now, we know that the circumference of the running track is the sum of the lengths of the two parallel straight lines and circumferences of two semi-circular ends. Now, we know that the circumference of a semi-circle is $\pi r$, where r is the radius of the semi-circle. So, we get,
$600\,m = \pi r + 200m + 200m + \pi r \\ $
Simplifying the calculation and adding up the like terms, we get,
$ \Rightarrow 600m = 400m + 2\pi r$
Now, shifting all the constants to the left side of the equation so as to find the value of r, we get,
$2\pi r = 600m - 400\,m \\ $
Carrying out the calculations, we get,
$2\pi r = 200\,m$
Dividing both sides of the equation by $2$, we get,
$\pi r = 100\,m \\ $
Now, substituting the value of $\pi $ in the equation, we get,
$\dfrac{{22}}{7} \times r = 100\,m$
\[ \Rightarrow r = 100\,m \times \dfrac{7}{{22}}\]
Cancelling the common factors in numerator and denominator, we get,
\[r = \dfrac{{350}}{{11}}\,m\]
\[ \therefore r = 31.82\,m\] (approx.)

Hence, the radius of the two semi-circular ends is \[31.82\,m\] approximately.

Note:We must know the formula for the circumference of a semicircle in order to solve the given problem. We must know simplification rules and transposition so as to simplify and solve the equation obtained. Always convert the final answer into decimal instead of leaving in fraction form. We must take care while doing calculations so as to be sure of the final answer.