Question

The diagram shows a windscreen wiper cleaning a car windscreen.

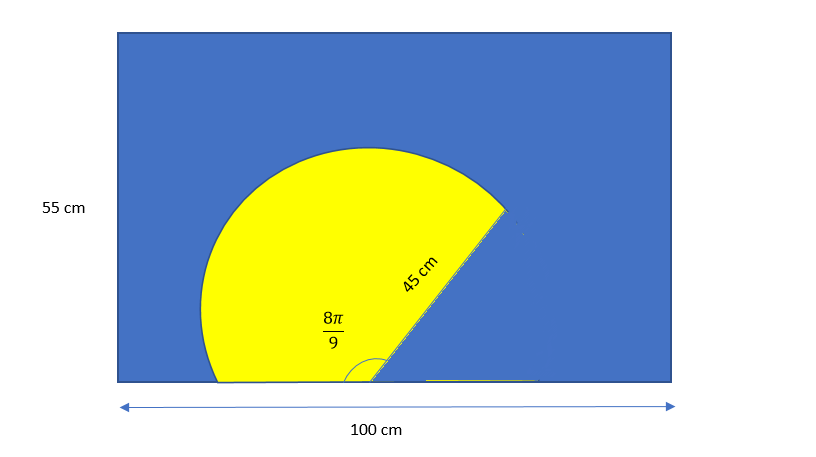
What is the length of the arc swept out?
What area of the windscreen is not cleaned?

Answer 1

Hint: We will first write the formulas of the length of arc and the area of a sector using the given radius. After that, we can directly find the length of the arc and the area of the windscreen not cleared can be found by the area of the total windscreen – the area cleaned.

Complete step-by-step answer:
Let us first of all discuss the formulas we are going to require in this solution.
Arc length is given by: $l = \theta r$, where $\theta $ is the angle in radians and r is the radius. ……….(1)
Area of a sector is given by: $Area = \dfrac{1}{2}\theta {r^2}$, where $\theta $ is the angle in radians and r is the radius. ..(2)
Now, since we are already given that the angle up to which the wiper has cleaned the window is
$\dfrac{{8\pi }}{9}$.
Part (i):
Since, we can also observe that the length of the radius is 45 cm as mentioned in the figure, so putting these information in equation number 1, to obtain:-
$ \Rightarrow $Arc length = $\dfrac{{8\pi }}{9} \times 45$ cm
Putting the value of $\pi $ as $\dfrac{{22}}{7}$, we will get:-
$ \Rightarrow $Arc length = $\dfrac{8}{9} \times 45 \times \dfrac{{22}}{7}$ cm
Simplifying the calculations in the above expression, we will get:-
$ \Rightarrow $Arc length = $\dfrac{{880}}{7}$ cm
Part (ii):
Since, we can also observe that the length of the radius is 45 cm as mentioned in the figure, so putting these information in equation number 2, to obtain:-
$ \Rightarrow $Area = $\dfrac{1}{2} \times \dfrac{{8\pi }}{9} \times {\left( {45} \right)^2}c{m^2}$
Putting the value of $\pi $ as $\dfrac{{22}}{7}$, we will get:-
$ \Rightarrow $Area = $\dfrac{1}{2} \times \dfrac{8}{9} \times {\left( {45} \right)^2} \times \dfrac{{22}}{7}c{m^2}$
Simplifying the calculations in the above expression, we will get:-
$ \Rightarrow $Area = $\dfrac{{19800}}{7}c{m^2}$ ………………(3)
This is the area of the window that has been cleaned. Now, let us find the area of whole window:
We know that the area of the rectangle is length and breadth.
So, the area of the windscreen = 5500 square cm. ……………(4)
Subtracting 3 from 4, we have:-
Area of windscreen that has not been cleaned = $\left( {5500 - \dfrac{{19800}}{7}} \right)c{m^2}$
Area of windscreen that has not been cleaned = $\dfrac{{18700}}{7}c{m^2}$.

Note:
The students must note that these formulas are derived from general formulas where angle was in degrees only, we have just converted the angle from degrees into radians.
If the angle is to be taken in degrees, then the arc length is given by:
$ \Rightarrow l = \dfrac{\theta }{{360}} \times 2\pi r$
Since, we know that $\pi = {180^ \circ }$
So, 1 radian = \[\dfrac{{{{180}^ \circ }}}{\pi }\]
And $\theta $ radians = \[\dfrac{{{{180}^ \circ }}}{\pi } \times \theta \] and now if you put these in the above, you will get the formula we used in the solution.
If the angle is to be taken in degrees, then the area of sector is given by:
$ \Rightarrow Area = \dfrac{\theta }{{360}} \times \pi {r^2}$