Question

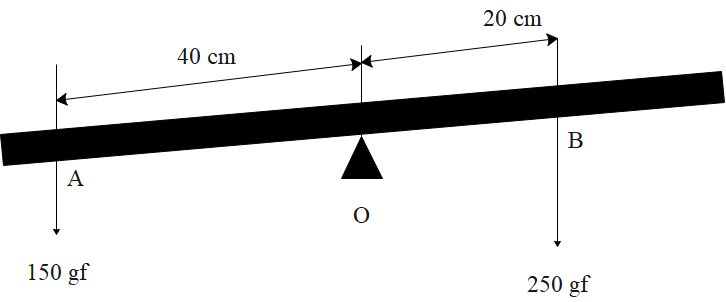
The diagram shows a uniform metre rule weighting 100 gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B on the metre rule such that OA = 40 cm and OB = 20 cm. Calculate:
(A) The total anticlockwise moment about O;
(B) The total clockwise moment about O;
(C) The total clockwise and anticlockwise moments; and
(D) The distance from O where a 100 gf weight should be placed to balance the metre rule.

Answer 1

Hint: To answer this question we should write the answer step by step. At first we have to begin the answer by considering the weight and the distance to calculate the total anticlockwise and clockwise moment respectively. Then the total will be obtained by the subtraction of the two. Ultimately the fourth subpart can be solved using the concept of principle of moments.

Complete step by step answer:
1. Let us solve the question by sub-parts. So here it goes:
We know that the total anticlockwise moment about O is given by:
$
  {\text{6000 gf cm = 5000 gf cm + 100 gf }} \times {\text{ d}} \\
   \Rightarrow {\text{1000 gf cm = 100 gf }} \times {\text{d}} \\
   \Rightarrow {\text{d = }}\dfrac{{{\text{1000 gf cm}}}}{{{\text{100 gf}}}}{\text{ = 10 cm on the right side of O}} \\
 $

Hence the total anticlockwise moment about O is 6000 gf cm.

2. We know that the total clockwise moment about O is given by:
${\text{250 gf }} \times {\text{ 20 cm = 5000 gf cm}}$

Hence the total clockwise moment about O is 5000 gf cm.

3. We know that the difference of anti clockwise and the clockwise moment is given by:
(6000 - 5000) gf cm = 1000 gf cm

Hence the total clockwise and anticlockwise moments is 1000 gf cm.
We know that from the principle of moments,
Anti clockwise moment = clockwise moment
Hence we know that to balance it, 100 gf weight has to be kept on the right hand side so as to produce an equal amount of clockwise moment about the point O.
Let us consider the distance from the point O be d cm.
Then we can write that:
${\text{150 gf }} \times {\text{ 40 cm = 250 gf }} \times {\text{ 20 cm + 100 gf }} \times {\text{ d}}$
So on the evaluation of the above expression is:
$
  {\text{6000 gf cm = 5000 gf cm + 100 gf }} \times {\text{ d}} \\
   \Rightarrow {\text{1000 gf cm = 100 gf }} \times {\text{d}} \\
   \Rightarrow {\text{d = }}\dfrac{{{\text{1000 gf cm}}}}{{{\text{100 gf}}}}{\text{ = 10 cm on the right side of O}} \\
 $
Hence we can say that 100 gf weight should be placed at 10 cm on the right side of O to balance the metre rule.

Note: We should know that moment is defined to be an expression which involves the product between the distance and that of the physical quantity. It totally depends on the orientation of the physical quantity. Moment is expressed in both clockwise and anti clockwise ways. The reference point should be chosen on the body that is taken into consideration. This point is also known as the pivot point on the object.