Question

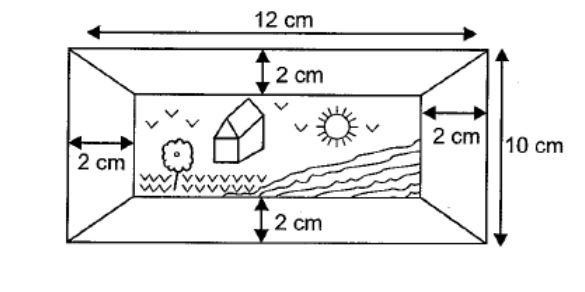
The diagram shows a framed picture. Find the area of the picture.

A) \[48c{m^2}\]
B) \[39c{m^2}\]
C) \[92c{m^2}\]
D) \[120c{m^2}\]

Answer 1

Hint: In this question first we will find the dimensions of the picture by adding or subtracting certain values and then substitute the values of the sides into the formula for area of a rectangular portion to get the desired answer.

Complete step by step solution:
Here we are given the following figure:

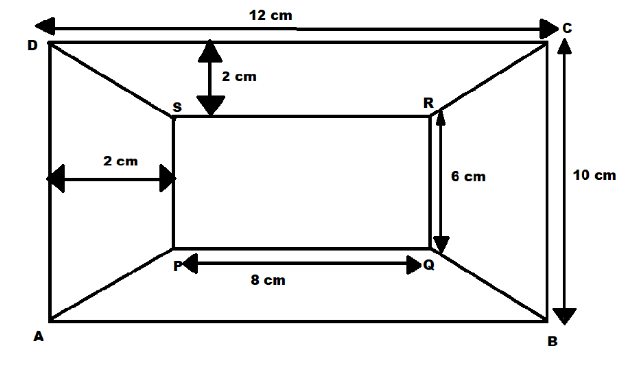
Let the frame be ABCD and the picture be PQRS
Then we have to find the dimensions of rectangle PQRS in order to find the area of the picture.
Therefore, first we will find the length (PS or RQ) of the picture:
Since it is given that length of AD or BC is 10 cm
Then in order to get the length of PS we need to subtract 2cm from both above and bottom
Therefore, length of PS is given by:
\[
  PS = 10 - 2 - 2 \\
  PS = 10 - \left( {2 + 2} \right) \\
  PS = 10 - 4 \\
  PS = 6cm \\
 \]
And since it is a rectangular picture, therefore length of opposite sides are equal
Hence, \[RQ = 6cm\]
Hence the length of the picture is 6 cm………………………………………..(1)
Now we have to find the breadth of the rectangle picture PQRS.
Since it is given that the length of AB or DC is 12 cm.
Then in order to get the length of PQ we need to subtract 2cm from both the sides
 Therefore, length of PQ is given by:
\[
  PQ = 12 - 2 - 2 \\
  PQ = 12 - \left( {2 + 2} \right) \\
  PQ = 12 - 4 \\
  PQ = 8cm \\
 \]
And since it is a rectangular picture, therefore length of opposite sides are equal
Hence, \[RS = 8cm\]
Hence the breadth of the picture is 8 cm……………………………..(2)
From (1) and (2) we get the length and breadth of the picture hence we will now calculate the area of the picture:
The area of rectangle is given by:
A = l $\times$ b

Hence in order to find the area of the picture PQRS we have to substitute the values of its length and breadth.
Hence, substituting the values we get:
\[
  {\text{Area = }}6 \times 8 \\
  {\text{Area = }}48c{m^2} \\ \]
Therefore the area of the picture is \[48c{m^2}\]. Hence A is the correct option.

Note:
The area of a rectangle is given by:
A = l $\times$ b
Also, the opposite sides of a rectangle are always equal.