Question

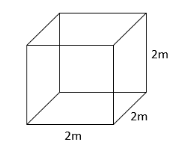
The diagram shows a box in the shape of a cube of lengths 2m. The box is packed with cubes of lengths \[1{\text{ }}cm\] . How many cubes does it hold?

A. 8000
B. 8000000
C. 4000000
D. 40000

Answer 1

Hint: We have to assume that the smaller cubes are placed inside the bigger cube in an arranged and even manner. And only then can we assume that the total volume of smaller cubes is equal to the volume of a bigger cube.

Complete step-by-step answer:
We are given a box in the shape of a cube of lengths 2m and the box is packed with cubes of lengths 1cm.
We have to assume that the smaller cubes are evenly arranged inside the bigger cube i.e. there is no void or empty space inside the bigger cube.
Once we assume this, it is justified that the total volume of smaller cubes will be equal to the volume of the bigger cube.
Firstly we will calculate the volume of the bigger cube.
Volume of cube = ${l^3}$ , where $l$ is length of the side …………. (1)
Using equation (1) we can find the volume –
Volume of bigger cube = ${(2m)^3} = 8{m^3} = 8 \times {10^6}c{m^3}$ …………… ($1{m^3} = {10^6}c{m^3}$)
Secondly assume that the total number of small cube be $x$
Using equation (1) we can find the volume –
Volume of one small cube = ${l^3} = {(1cm)^3} = 1c{m^3}$
Total volume of $x$small cubes = $1c{m^3} \times x = xc{m^3}$
Since, the volume of smaller cubes will be equal to one bigger cube we get –
$\begin{gathered}
   \Rightarrow xc{m^3} = 8 \times {10^6}c{m^3} \\
   \Rightarrow x = 8000000 \\
\end{gathered} $

Therefore, option (b) is the correct option.

Note: While equating the volumes we must take care of the unit. If the units are the same then volumes can be directly equated whereas if different then need to be converted first.