Question

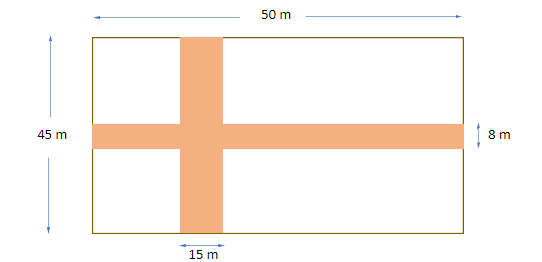
The diagram given below shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The width of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.

Answer 1

Hint: We are given a condition where two paths intersect with each other inside a rectangular field whose length and width are given and we have to find the area of the shaded portion in the figure. We will find the area of the shaded rectangular paths individually by the formula of the area of the rectangle = length of the rectangle$ \times $breadth of the rectangle and add both of them and then we will subtract the area of the common portion from the combined area to finally get the area of the required shaded region.

Complete step-by-step answer:
We have a rectangular field with its length and breadth given as: length = 80 m and breadth = 45 m.
There are two paths crossing each other and their width has been given as 8 m and 15 m as in the figure:

Let us first calculate the area of the rectangular path with length 50 m and width 8 m.
Area of the path 1 = length $ \times $width = 50 m$ \times $ 8 m = 400 ${m}^{2}$
Now, for the area of path 2 with length 45 m and width 15 m, we have
Area of the path 2 = length $ \times $ width = 45 $ \times $15 = 675 ${m}^{2}$
For the area of the common portion, we have length = 15 m and width = 8 m.
Therefore, area of common part = length $ \times $ width = 15$ \times $8 = 120 ${m}^{2}$
So, we can now calculate the area of the shaded portion given by the formula:
Area of shaded region= area of path1 + area of path2 – area of common part = 400+675–120 =955 ${m}^{2}$
Therefore, the area of the shaded region is found to be 955 ${m}^{2}$

Note: Such problems are usually figure dependent. So, you should try to analyse the diagram because many times you forget about the area being included twice just as in this question.