Question

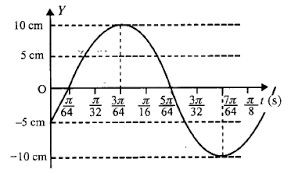
The diagram below shows a sinusoidal curve. The equation of the curve will be:

Answer 1

Hint
We will use the equation of sinusoidal curve given by: -
$\Rightarrow y = A\operatorname{Sin} (wt + \phi )$
Where, Y = Displacement of the wave in y-axis.
A = Amplitude/Maximum Displacement of the wave.
w = angular velocity of the wave.
t = time passed.
$\phi $ = initial phase angle.
Next, we will obtain these values by observing the figure and at last substitute them in the equation of the curve.

Complete step by step answer
The equation for a sinusoidal curve is represented by the following expression: -
 $y = A\operatorname{Sin} (wt + \phi )$
Where, Y = Displacement of the wave in y-axis.
A = Amplitude/Maximum Displacement of the wave.
w = angular velocity of the wave.
t = time passed.
$\phi $ = initial phase angle.
Now, from the figure we observe:
Amplitude(A) = 10 cm
Next, we will calculate the Time period (T) of the wave. T is the time taken by the wave to complete one oscillation. According to the figure, the wave completes half of its oscillation in $ \left( {\dfrac{{5\pi }}{{64}} - \dfrac{\pi }{{64}}} \right)$ seconds. Thus, we can write: -
 $\Rightarrow \dfrac{T}{2} = \left( {\dfrac{{5\pi }}{{64}} - \dfrac{\pi }{{64}}} \right)$
 $\Rightarrow \dfrac{T}{2} = \dfrac{{4\pi }}{{64}} = \dfrac{\pi }{{16}}$
 $\Rightarrow \therefore T = \dfrac{\pi }{8}$
Now, using formula, $w = \dfrac{T}{{2\pi }}$
Where, $\omega$ = angular velocity, T = time period of the wave.
Angular velocity becomes: -
 $\Rightarrow w = \dfrac{{2 \times 8 \times \pi }}{\pi } = 16$
Now, putting these values into the equation of wave we get: -
 $\Rightarrow y = 10\operatorname{Sin} (16t + \phi )$
Now, for $y = 10$ cm, $t = \dfrac{{3\pi }}{{64}}$ from the diagram. We will put these values into the above equation to calculate the initial phase angle.
 $\Rightarrow 10 = 10\operatorname{Sin} \left( {16 \times \dfrac{{3\pi }}{{64}} + \phi } \right)$
 $ \Rightarrow \operatorname{Sin} \left( {\dfrac{{3\pi }}{4} + \phi } \right) = 1$
Comparing it with $\operatorname{Sin} \left( {\dfrac{\pi }{2}} \right) = 1$ , we can write: -
 $\dfrac{{3\pi }}{4} + \phi = \dfrac{\pi }{2}$
 $ \Rightarrow \phi = \dfrac{\pi }{2} - \dfrac{{3\pi }}{4} = \dfrac{{ - \pi }}{4}$
Finally, we will put all these values into the equation to obtain the required equation of wave.
 $ \Rightarrow y = 10\operatorname{Sin} \left( {\dfrac{{3\pi }}{4}t - \dfrac{\pi }{4}} \right)$
Hence, the equation of curve will be $y = 10\operatorname{Sin} \left( {\dfrac{{3\pi }}{4}t - \dfrac{\pi }{4}} \right)$ .

Note
As the value for $\operatorname{Sin} \left( {\dfrac{{3\pi }}{2}} \right)$ is also equal to one.
Comparing $\operatorname{Sin} \left( {\dfrac{{3\pi }}{4} + \phi } \right) = 1$ with $\operatorname{Sin} \left( {\dfrac{{3\pi }}{2}} \right) = 1$ we can write: -
 $ \Rightarrow \phi = \dfrac{{3\pi }}{2} - \dfrac{{3\pi }}{4} = \dfrac{{5\pi }}{4}$
Thus, the equation of wave becomes:
$ \Rightarrow y = 10\operatorname{Sin} \left( {\dfrac{{3\pi }}{4}t + \dfrac{{5\pi }}{4}} \right)$.
This is also correct. In fact, infinite such solutions can be obtained as the trigonometric function ‘Sin’ has its value equal to 1 for infinite values of x, all of these are correct. The student must mark the solution available in the options and is suggested to use principal values of the Sin function to avoid large numbers in the equation.