Question

The diagram below shows a metric scale balanced at $ 30cm $ mark. State which of the following options is true and why?

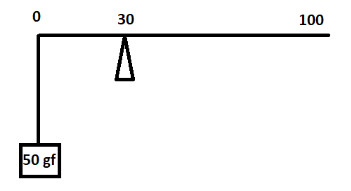
(A) Weight of the scale $ > 50gf $
(B) Weight of the scale $ < 50gf $
(C) Weight of the meter scale $ = 50gf $

Answer 1

Hint: The above problem can be solved using the principle of moments. The principle of moments can be stated as “when the system is in equilibrium then we can say that the sum of its anti-clockwise moments will be equal to the sum of its clockwise moments. We need to recall the formula for the moment of force and then we need to substitute the values to get the answer.

Complete Step By Step Answer:
Using the principle of moments we are going to find the weight of the scale. The principle of moments can be written mathematically as
 $ {\tau _1} = {\tau _2} $
Here $ {\tau _1} $ is the anti-clockwise moment and $ {\tau _2} $ is the clockwise moment. We know the formula for the moment of force that is given by,
 $ \tau = F \times d $
Here, $ F $ is the force applied and $ d $ is the distance from the fixed axis.
According to Newton’s law of motion, we know that,
 $ F = mg = w $
Here $ w $ is the weight of the object
Therefore we get,
 $ \tau = w \times d $
The anti-clockwise moment can be found by,
 $ \Rightarrow {\tau _1} = 50gf \times 30 $ …… (1)
The clockwise moment can be found by,
 $ {\tau _2} = w \times 100 $ …… (2)
Therefore according to the principle of moments, we can equate equations (1) and (2) we get,
 $ 50gf \times 30 = w \times 100 $
Rearranging the above equation we get,
 $ \Rightarrow 50gf \times \dfrac{{30}}{{100}} = w $
Solving this we will arrive at the weight of the meter scale.
 $ w = 15gf $ .
Therefore the weight of the scale $ < 50gf $
Correct Answer: Therefore the correct option is $ B $ .

Note:
The moment of force formula can be applied to calculate the moment of force for balanced as well as unbalanced force. The SI unit for the moment is given $ kg{m^2}{\text{/}}{s^2} $ . We can also express the moment of force in terms of Nm. The measure of the tendency to make a body to rotate about a given specific axis is defined as the moment of force.