Question

The diagonals of the three faces of a cuboid are x, y, z respectively. What is the volume of the cuboid?
A. $\dfrac{{xyz}}{{2\sqrt 2 }}$
B. $\dfrac{{\sqrt {\left( {{y^2} + {z^2}} \right)\left( {{z^2} + {x^2}} \right)\left( {{x^2} + {y^2}} \right)} }}{{2\sqrt 2 }}$
C. $\dfrac{{\sqrt {\left( {{y^2} + {z^2} - {x^2}} \right)\left( {{z^2} + {x^2} - {y^2}} \right)\left( {{x^2} + {y^2} - {z^2}} \right)} }}{{2\sqrt 2 }}$
D. None of the above.

Answer 1

Hint: To solve this question, we will use the concept of surface area and volume of a cuboid. The volume of a cuboid is given by $l \times b \times h$, where l, b and h are respectively the length, breadth and height of the cuboid. We will also use the Pythagoras theorem, i.e. \[{\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2}{\text{ + }}{\left( {{\text{base}}} \right)^2}\].

Complete step-by-step answer:
Given that,
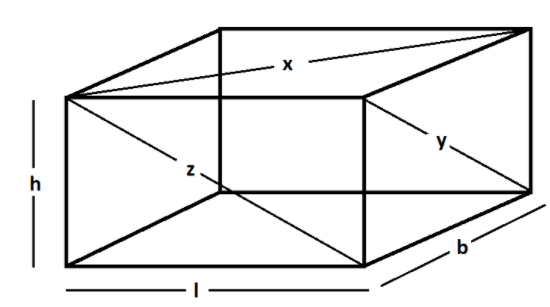
x, y and z are the diagonals of the three faces of a cuboid.
Let l, b and h are respectively be the length, breadth and height of the cuboid.
We will apply the Pythagoras theorem on these three faces of the cuboid.
From the figure, we can see that
$ \Rightarrow {x^2} = {l^2} + {b^2}$ ……….. (i)
$ \Rightarrow {y^2} = {b^2} + {h^2}$ ………… (ii)
$ \Rightarrow {z^2} = {l^2} + {h^2}$ ………… (iii)
Now, we have to make some relations using these equations so that we can find out the values of l, b and h.
Adding equation (i) and (ii), we will get
$
   \Rightarrow {x^2} + {y^2} = {l^2} + {b^2} + {b^2} + {h^2} \\
   \Rightarrow {x^2} + {y^2} = {l^2} + 2{b^2} + {h^2} \\
$
Now subtract equation (iii) from equation (iv)
$
   \Rightarrow {x^2} + {y^2} - {z^2} = {l^2} + 2{b^2} + {h^2} - {l^2} - {h^2} \\
   \Rightarrow {x^2} + {y^2} - {z^2} = 2{b^2} \\
$
From this, we will get
$ \Rightarrow b = \sqrt {\dfrac{{{x^2} + {y^2} - {z^2}}}{2}} $ ………… (v)
Similarly, adding equation (i) and (iii) and subtracting (ii) from it, we will get
$ \Rightarrow {x^2} + {z^2} - {y^2} = 2{l^2}$
From this, we will get
\[ \Rightarrow l = \sqrt {\dfrac{{{x^2} + {z^2} - {y^2}}}{2}} \] ……….. (vi)
Now, adding equation (ii) and (iii) and subtracting equation (i) from it, we will get
$ \Rightarrow {y^2} + {z^2} - {x^2} = 2{h^2}$
From this, we will get
\[ \Rightarrow h = \sqrt {\dfrac{{{y^2} + {z^2} - {x^2}}}{2}} \] ………… (vii)
Here, we have found the values of l, b and h.
We know that,
Volume of cuboid = $l \times b \times h$
Putting the values from equation (v), (vi) and (vii), we will get
$ \Rightarrow $ Volume of cuboid = $\sqrt {\dfrac{{{x^2} + {z^2} - {y^2}}}{2}} \times \sqrt {\dfrac{{{x^2} + {y^2} - {z^2}}}{2}} \times \sqrt {\dfrac{{{y^2} + {z^2} - {x^2}}}{2}} $
$ \Rightarrow $ Volume of cuboid = $\dfrac{{\sqrt {\left( {{y^2} + {z^2} - {x^2}} \right)\left( {{z^2} + {x^2} - {y^2}} \right)\left( {{x^2} + {y^2} - {z^2}} \right)} }}{{2\sqrt 2 }}$
Hence, the correct answer is option (C).

Note:Whenever we ask such questions, we have to remember some basic points regarding the volume of a cuboid. First, we have to make some equations by applying the Pythagoras theorem using the given details. Then we have to solve those equations in order to get the value of l, b and h of the cuboid. After that, by putting those values simply in the formula of volume of a cuboid, we will get the required answer.