Question

The diagonals of the quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Draw a rough figure to justify your answer.

Answer 1

Hint: Try thinking about the shape of a kite. Where we have two sticks crossing each other perpendicularly in the middle of the kite. But all the sides are not necessarily equal for any kite.

Complete step-by-step answer:
No, if the diagonals of the quadrilateral are perpendicular to each other then such a quadrilateral is not always a rhombus.
As we know the conditions of rhombus,
1. It should always be a parallelogram.
2. All the sides of the quadrilateral should be equal.
3. The diagonals are perpendicular to each other.

So here given only, “Diagonals of the quadrilateral are perpendicular to each other.”
Hence, we can’t say a given quadrilateral is always rhombus.

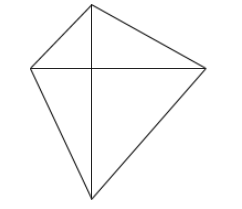
This is a quadrilateral with perpendicular diagonals which is not a rhombus.

Note: In some other cases also, we can think of some shape which has perpendicular diagonals without being a rhombus. Try exploring some other figures. You can also think that square is such a figure that it has perpendicular diagonals and it is not a rhombus. But you need to know that every square is a rhombus, so we can’t consider the case.