Question

The diagonals of a square are $ \_\_\_\_\_ $ .

Answer 1

Hint: As we know that square is a two dimensional figure with all the four sides equal. Each angle of the square is equal to $ {90^ \circ } $ . We can calculate the area of the square with the formula $ {(side)^2} $ . In this question we have to find the properties of the diagonals of the square, so we will draw the diagram and solve it.

Complete step-by-step answer:
Let us first draw a square ABCD.

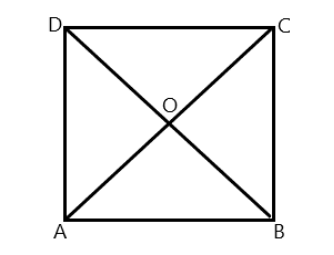
Here in the above image ABCD is a square with all of its equal i.e. $ AB = BC = CD = AD $ . O is the meeting point of the diagonals $ AC $ and $ BD $ .
Now we will solve it. In triangle ABC and DCB we have $ AB = DC $ , sides of a square are equal.
 $ \angle ABC = \angle DCB = {90^ \circ } $ and we have $ BC = BC $ , common in both the triangles.
So we can say that by Side-Angle-Side congruence, $ \Delta ABC \cong \Delta DCB $ .
Therefore we have $ AC = DB $ by the corresponding sides of the congruent triangles.
Hence from this we can say that the diagonals of the square are equal.
Now in triangle AOB and COD, we have $ \angle AOB = \angle COD $ (Vertically opposite angles).
 $ \angle ABO = \angle CDO $ , since Ab is parallel to CD and line BD is the transversal so the alternate angles are equal.
Also $ AB = CD $ , sides of the squares are equal.
Hence we can say that by SIDE-SIDE-SIDE congruence $ \Delta AOB \cong \Delta COB $ .
Therefore by the corresponding sides of the congruent triangle we have $ \angle AOB = \angle COB $ . From this we can say that the diagonals bisect each other.
Hence the diagonals of a square are equal and they bisect each other.

Note: Before solving this kind of question we should have the clear idea of square, their properties and the criteria of congruence . Such problems are always based on the concept of triangle congruence so we should always pick the correct pair of triangles and apply the concept of congruence and solve them.