Question

The diagonals of a rhombus bisect each other at right angles. Use this fact to find the area of a rhombus whose diagonals are of length 8 cm and 6 cm.

Answer 1

Hint: Here we will first use the given fact to state that the rhombus is divided into 4 triangles. Then we will find the side of that triangle and using the sides, we will calculate the area of the triangle. Then we will multiply the area of the triangle four times to get the area of the rhombus.

Complete step-by-step answer:
We know that the diagonals of a rhombus bisect each other at right angles, which means that the diagonals divide the rhombus into 4 equal triangles with sides equal to half the length of the diagonals.
Using this we will draw the diagram.

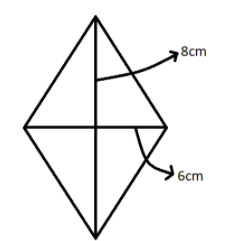
Now, first we will find the sides of those triangles, we get
Sides of the triangle formed by the bisection of the diagonals of the rhombus are \[\dfrac{8}{2} = 4cm\] and \[\dfrac{6}{2} = 3cm\].
Now we will find the area of the triangle which is equal to half of the product of base of the triangle and height of the triangle. Therefore, we get
Area of the triangle \[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height}}\]
Substituting 4 for base and 3 for height in the above formula, we get
\[ \Rightarrow \] Area of the triangle \[ = \dfrac{1}{2} \times 4 \times 3\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of the triangle \[ = 6{\rm{c}}{{\rm{m}}^2}\]
We know that the rhombus got divided into 4 such triangles. Therefore, the area of the rhombus is equal to 4 times the area of the triangle. Therefore, we get
Area of the rhombus \[ = 4 \times \]Area of triangle
Substituting 6 for area of triangle in the above equation, we get
\[ \Rightarrow \] Area of the rhombus \[ = 4 \times 6\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of the rhombus \[ = 24{\rm{c}}{{\rm{m}}^2}\]
Hence the area of the rhombus is equal to \[24{\rm{c}}{{\rm{m}}^2}\].

Note: Rhombus is a two-dimensional geometric shape which has 4 sides of equal length. It is a special case of parallelogram and the diagonals intersect each other at \[90^\circ \]. In rhombus, the opposite angles are equal and opposite sides are parallel. A square is a special case of rhombus as it has also equal sides and its diagonal bisect each other at \[90^\circ \].