Question

The diagonals of a rhombus are 16m and 12m, find:
(i) Its area
(ii) Length of a side
(iii) perimeter

Answer 1

Hint: A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram (written as gm).
A parallelogram having all sides equal is called a rhombus.
Properties of rhombus:
I.All sides of the rhombus are equal.
II.Opposite sides of a rhombus are equal.
III.Diagonals bisect each other at right angles.

Complete step-by-step answer:

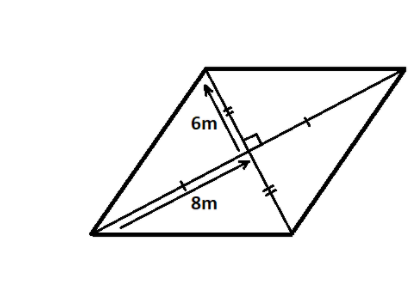
For the given rhombus let \[{{d}_{1}}\,=\,16\,m\] and \[{{d}_{2}}\,=\,12\,m\].
Now:
I.Area of Rhombus:
Area of a rhombus is given by:\[Area\,=\,\dfrac{1}{2}\,\times \,{{d}_{1}}\,\times \,{{d}_{2}}\]
where \[{{d}_{1}}\]is the length of one diagonal,\[{{d}_{2}}\] is the length of another diagonal.
Verification of formula:
This formula can easily be derived by observing the figure and using the property of rhombus that its diagonals bisects each other at right angles.
So, the rhombus can be divided into two triangles with base as \[{{d}_{1}}\] and height as \[{{d}_{2}}\].
Now, area of the rhombus = 2 \[\times \] Area of the triangles
= \[2\,\times \,\left( \,\dfrac{1}{2}\,\times \,{{d}_{1}}\,\times \,\dfrac{{{d}_{2}}}{2} \right)\]
= \[\,\dfrac{1}{2}\,\times \,{{d}_{1}}\,\times \,{{d}_{2}}\], Hence verified.
hence area of rhombus = \[\dfrac{1}{2}\,\times \,16m\times 12m\,\,=\,\,96\,{{m}^{2}}\].

II.Length of side:
As we know that the diagonals of a rhombus bisect each other at right angles so we can find the side length of the rhombus by using Pythagoras theorem.
Mathematically:
\[{{(side)}^{2}}\,=\,\,{{\left( \dfrac{{{d}_{1}}}{2} \right)}^{2}}\,+\,\,{{\left( \dfrac{{{d}_{2}}}{2} \right)}^{2}}\]
\[{{(side)}^{2}}\,\,=\,\,{{\left( 8 \right)}^{2}}\,\,+\,\,\,{{\left( 6 \right)}^{2}}\]
\[{{(side)}^{2}}\,=\,\,100\,\,=\,\,{{(10)}^{2}}\]
hence, length of side of the Rhombus = \[10\,m\].

III.Perimeter of rhombus:
Perimeter of shape means sum of length of all of its sides of that particular shape
In rhombus as its all four sides are equal, so its perimeter will be \[Perimeter\,=\,\,4\times length\,\,of\,side\]
\[\therefore \,\,Perimeter\,=\,\,4\times 10\,=\,\,40\,m\]

Note: While dealing with geometrical shapes one must remember all its properties, like relation between the sides, relation between angles, etc. A rhombus is a shape in which pairs of opposite sides are equal and adjacent sides are equal.