Question

The diagonals of a field in the form of a quadrilateral are 106 m and 80 m and intersect each other at right angles. Find the cost of cultivating the field at the rate of Rs. 25.50 per 100${m^2}$.
A.Rs. 1081.20
B.Rs. 981.20
C.Rs. 1181.20
D.Rs. 1020.34

Answer 1

Hint:: We will first divide the given quadrilateral into four triangles created by the diagonals of the quadrilateral. As the diagonals are perpendicular, so each triangle will be right angle triangle. We will determine the area of each triangle using the formula: $A = \dfrac{1}{2} \times b \times h$and then express the sum of areas of all four triangles in terms of its diagonals to find the area of the quadrilateral. After getting the area we will calculate the cost by the unitary method.

Complete step by step answer:

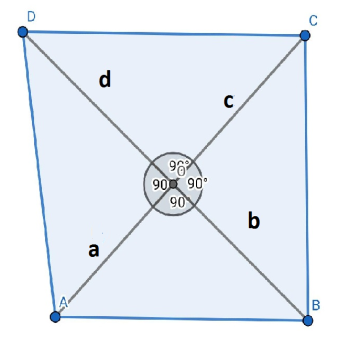
Consider ABCD to be the given quadrilateral.
Diagonals of a quadrilateral are line segments joining opposite vertices, so AC and BD are the diagonals. The diagonals intersect at O
As given, the diagonals of the field are 106 m and 80 m and intersect each other at right angles.
Let, $AC = 106m$ and $BD = 80m$
Let
$
  OA = a \\
  OB = b \\
  OC = c \\
  OD = d \\
  $
Now, as triangle OAB, OBC, OCD, ODA are right angled triangles,
Area of right angles triangle is half times the product of base and height
Or $A = \dfrac{1}{2} \times b \times h$
So,
$ar\left( {\Delta OAB} \right) = \dfrac{1}{2} \times OA \times OB$
$\Rightarrow ar\left( {\Delta OAB} \right) = \dfrac{1}{2} \times a \times b = \dfrac{{ab}}{2}$ …(i)
Similarly,
$ar\left( {\Delta OBC} \right) = \dfrac{1}{2} \times OC \times OB$
$\Rightarrow ar\left( {\Delta OBC} \right) = \dfrac{1}{2} \times c \times b = \dfrac{{cb}}{2}$ …(ii)
$ar\left( {\Delta OCD} \right) = \dfrac{1}{2} \times OC \times OD$
$\Rightarrow ar\left( {\Delta OCD} \right) = \dfrac{1}{2} \times c \times d = \dfrac{{cd}}{2}$ …(iii)
$ar\left( {\Delta OAD} \right) = \dfrac{1}{2} \times OA \times OD$
$\Rightarrow ar\left( {\Delta OAD} \right) = \dfrac{1}{2} \times a \times d = \dfrac{{ad}}{2}$ …(iv)
Now, area of quadrilateral is equal to the sum of all four triangles.
Thus, \[ar\left( {ABCD} \right) = ar\left( {\Delta OAB} \right) + ar\left( {\Delta OBC} \right) + ar\left( {\Delta OCD} \right) + ar\left( {\Delta OAD} \right)\]
Using (i), (ii), (iii) and (iv), we get
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{ab}}{2} + \dfrac{{bc}}{2} + \dfrac{{cd}}{2} + \dfrac{{ad}}{2}\]
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{ab + bc + cd + ad}}{2}\]
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{b\left( {a + c} \right) + d\left( {c + a} \right)}}{2}\]
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{\left( {b + d} \right)\left( {a + c} \right)}}{2}\]
Now, we will substitute back the values of a, b, c, d in the above equation,
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{\left( {OB + OD} \right)\left( {OA + OC} \right)}}{2}\]
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{\left( {BD} \right)\left( {AC} \right)}}{2}\]
Now, we have the area of quadrilateral in terms of its diagonals.
As given, $AC = 106m$ and $BD = 80m$
$\Rightarrow$ \[ar\left( {ABCD} \right) = \dfrac{{\left( {80} \right)\left( {106} \right)}}{2}{m^2}\]
$\Rightarrow$ \[ar\left( {ABCD} \right) = 4240{m^2}\]
Thus, the area of quadrilateral is \[4240{m^2}\]
Now, cost of cultivating the field is: Rs. 25.50 per 100${m^2}$
So, cost of cultivating 100${m^2}$is: Rs. 25.50
$\Rightarrow$ Cost of cultivating 1${m^2}$is: Rs. $\dfrac{{25.50}}{{100}}$
$\Rightarrow$ Cost of cultivating \[4240{m^2}\] is: Rs. $\dfrac{{25.50}}{{100}} \times 4240 = $Rs. 1081.20
Hence, the cost of cultivating the field is Rs. 1081.20, so the option A Rs. 1081.20 is correct

Note:: Students must be aware that the given quadrilateral has only perpendicular diagonals, so not to consider it as a rhombus or a square unless it is mentioned so.
A square is a 2D figure with perpendicular diagonals, but it also has all sides equal and adjacent sides perpendicular.
A rhombus is a 2D figure with perpendicular diagonals, but it also has all sides equal.
So when only it’s given that diagonals are perpendicular, students must assume an arbitrary quadrilateral.