Question

The diagonal of a square A is (x + y). The diagonal of square B with twice the area of A is-
$
  A\sqrt 2 \left( {x + y} \right) \\
  B{\text{ 2}}\left( {x + y} \right) \\
  C{\text{ 2x + 4y}} \\
  {\text{D 4x + 2y}} \\
 $

Answer 1

Hint- Here we will proceed by using the given condition i.e. diagonal of square A = x + y, we will find area of both the squares so that we can get the side of square B. Then using the formula of diagonal of square i.e. $\sqrt 2 a$, we will get the required diagonal of square.

Complete step-by-step answer:

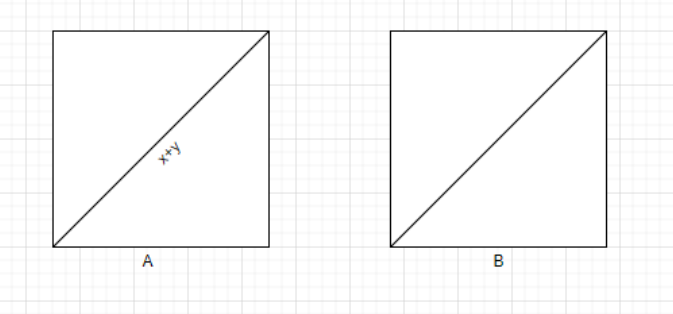
As we are given that diagonal of square A = x + y
Now let us assume a be the side of square A,
Also $2{a^2} = {\left( {x + y} \right)^2}$
According to the question,
We can say that area of square B $ = 2{a^2}$
(As area of B $ = 2 \times area{\text{ of A}}$)
Area of B $ = {\left( {x + y} \right)^2}$
But we know that the formula of area of square is ${\left( {side} \right)^2}$
So each side of the square B $ = \left( {x + y} \right)$
And by using the formula of diagonal of square $ = \sqrt 2 a$
We get-
Diagonal of square B $ = \sqrt 2 \left( {x + y} \right)$

Note- In order to solve this type of question, we must know all the formulas related to square as here also we used the formula of area of square i.e. ${\left( {side} \right)^2}$and formula of diagonal of square$ = \sqrt 2 a$.