Question

The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.

Answer 1

Hint: We will use the Pythagoras theorem: ${\text{hypotenus}}{{\text{e}}^2} = {\text{bas}}{{\text{e}}^2}{\text{ + perpendicula}}{{\text{r}}^2}$ in the triangle formed by diagonal and two sides (shorter and longer) of the rectangle to solve this question. We will write the diagonal and the longer side in terms of the shorter side for simplicity in calculation.

Complete step-by-step answer:
We are given that a rectangular field has the diagonal 60 metres more than the shorter side and longer side, 30 metres more than the shorter side.
Let the shorter side be of x metres.
We can write the diagonal in terms of the shorter side as: $60 + x$
And, the longer side can be written as: $30 + x$
Now, looking at the diagram of the field:

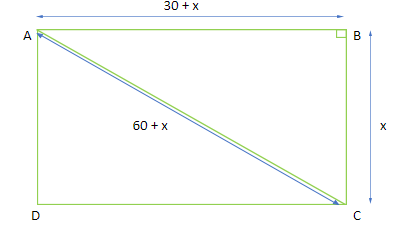
We know that all angles (vertex) of the rectangle are of ${90^ \circ }$ . Therefore, applying Pythagoras theorem in the right triangle ABC, we get
$ \Rightarrow {\text{hypotenuse}}{{\text{e}}^2} = {\text{bas}}{{\text{e}}^2}{\text{ + perpendicular}}{{\text{r}}^2}$
$ \Rightarrow {\left( {60 + x} \right)^2} = {\left( {30 + x} \right)^2} + {x^2}$
Expanding the terms using the algebraic identity ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$
$
   \Rightarrow 3600 + {x^2} + 120x = 900 + {x^2} + 60x + {x^2} \\
   \Rightarrow {x^2} - 60x - 2700 = 0 \\
 $
Factoring the above equation, we get
$
   \Rightarrow {x^2} + 30x - 90x - 2700 = 0 \\
   \Rightarrow x\left( {x + 30} \right) - 90\left( {x + 30} \right) = 0 \\
   \Rightarrow \left( {x - 90} \right)\left( {x + 30} \right) = 0 \\
 $
$ \Rightarrow x = 90{\text{ or }}x = - 30$
We get two values of the shorter side, x as 90 or -30. Now, we know that the length can’t be negative, hence, the value of the shorter side will be x = 90 metres.
Substituting the value of x in the length of longer side, we get
$ \Rightarrow x + 30 = 90 + 30 = 120$
Therefore, the length of the longer side of the rectangle is 120 metres.
Hence, the sides of the field are 90 m and 120 m.

Note: In this question, you may get confused while deducing the relations between the sides and then using the Pythagoras theorem in triangle ABC. We have used the splitting the middle term factorization method to solve for the values of x. It is the method in which we split the middle term (the term having x) such that the sum of those splitted terms is equal to the middle term as well as the product of the other two terms other than mid-term (the term having $x^2$ and the constant term).