Question

The diagonal of a rectangular field is \[60\] metres more than the shorter side. If the longer side is \[30\] metres more than the shorter side, find the sides of the field.

Answer 1

Hint: In this question we have to find the sides of the field by using the given conditions. The given is the length of the diagonal of a rectangular field and relation among the diagonal of a rectangular field, longer side and shorter side.
First we take one random variable as the shorter side. Then applying the given condition we can find the longer side also.
Also from the condition for the diagonal applying Pythagoras theorem we can find the value of the random variable.

Complete step-by-step answer:
Let, the shorter side $BC$ of the field = \[x\] metre
Then, the longer side $AB$ of the field = \[x + 30\] metre
Diagonal $AC$ of the field =\[x + 60\] metre
               

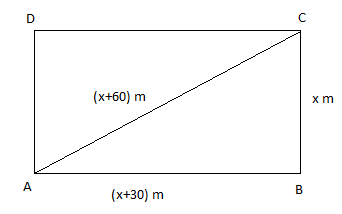
Now, in the right angled \[\Delta ABC\], applying Pythagoras theorem we have,
\[ \Rightarrow A{C^2} = A{B^2} + B{C^2}\]
Substituting the values of the sides,
\[ \Rightarrow {(x + 60)^2} = {(x + 30)^2} + {x^2}\]
Using algebraic identity formula ${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$,
\[ \Rightarrow {x^2} + 120x + 3600 = {x^2} + 60x + 900 + {x^2}\]
Simplifying the above equation we get,
\[ \Rightarrow {x^2} - 60x - 2700 = 0\]
This is quadratic equation we will solve this my middle term factor,
\[ \Rightarrow {x^2} - 90x + 30x - 2700 = 0\]
Splitting the above equation into two terms,
\[ \Rightarrow x(x - 90) + 30(x - 90) = 0\]
Solving the above we get,
\[ \Rightarrow (x - 90)(x + 30) = 0\]
\[ \Rightarrow x = 90 {\text{or}} - 30\]
Thus, the shorter side of the field is \[90\] metre.
The longer side of the field =\[90 + 30 = 120\] metre.
Hence the two sides of the rectangular field is \[90\] metre and \[120\] metre.

Note: A rectangle is a 2D shape in geometry, having four sides and four corners. Its two sides meet at right angles. Thus, a rectangle has four angles, each measuring \[90^\circ \]. The opposite sides of a rectangle have the same lengths and are parallel.
\[{\text{Area of the rectangle}} = Length \times breadth\]
Pythagoras theorem states that,
If \[ABC\] is a right angled triangle then,
\[A{C^2} = A{B^2} + B{C^2}\]
Also, Quadratic equation can be solved by splitting the middle term and then making it a multiplication of two factors, solving these two we get the solution.